
A Bigint Calculator
(9 May 2016)
This is a programming exercise I've wanted to do for a long time: an implementation of arbitrary-precision integer ("bigint") arithmetic in C.
Computers have instructions for doing arithmetic on binary numbers of certain sizes, most commonly 32 or 64 bits. The largest 32-bit number is 2^32-1, or 4,294,967,295; computations on larger numbers have to be performed in multiple steps operating on smaller pieces.
This is similar to how humans compute: we can handle numbers up to a certain size in our heads, but for larger numbers, we use methods that break the computation into smaller steps. For example, to calculate 5678 + 9012, we might use pen and paper to add one decimal position at a time from right to left, "carrying the one" as necessary.
Those same methods, or algorithms, we learned at school are used by computers as well (and computers are usually better at executing them than we are). This post shows implementations of these algorithms, and how they can be used to build a simple calculator.
Table of Contents
The Classical Algorithms
Don Knuth gives formal descriptions of the "schoolbook" algorithms for long arithmetic in The Art of Computer Programming Vol 2, Section 4.3.1: "The Classical Algorithms".
These algorithms are classical in a whole different sense than, for example, Quicksort; they are classical as in being many hundreds of years old (see for example David E. Smith History of Mathematics, Vol II).
Our implementation represents numbers as arrays of unsigned 32-bit integers. This is simlar to our usual positional number system, except instead of each position having a digit from 0 to 9, it now has a value from 0 to 2^32-1. The least significant position is at array index zero.
Note: this implementation uses variable-length arrays (VLAs) in some places. That means it is not suitable for production use unless the inputs are known to always fit on the stack.
Addition

This is the most straight-forward of the four operations. The numbers are added one position at the time, starting from the least significant position. If an intermediate sum is greater or equal to the base, a one is carried to the next position.
/* Add n-place integers u and v into (n + 1)-place w. */
static void algorithm_a(int n, const uint32_t *u, const uint32_t *v,
uint32_t *w)
{
bool carry, carry_a, carry_b;
uint32_t sum_a, sum_b;
int j;
carry = false;
for (j = 0; j < n; j++) {
sum_a = u[j] + carry;
carry_a = (sum_a < u[j]);
sum_b = sum_a + v[j];
carry_b = (sum_b < sum_a);
w[j] = sum_b;
assert(carry_a + carry_b <= 1);
carry = carry_a + carry_b;
}
w[j] = carry;
}
The tricky part is dealing with the carries. C does not provide an "add with carry" operation, so we need to carefully perform it ourselves, first adding the incoming carry to one of the operands, and then the second operand to the result. The operations need to be done separately, as either one can overflow (but never both at the same time), yielding an outgoing carry.
At the machine language level, computers typically do have instructions for add with carry, so one could hope that the compiler would use them for this code. However, none of the X86 compilers I tried does so (the same is true for subtract with borrow).
One way to get the instruction we want is of course to implement the algorithm in assembly. The GNU Multi Precision Arithmetic Library (GMP), the gold standard in bignum arithmetic, does precisely this for many of its algorithms. For addition, the X86 implementation of mpn_add_n jumps into an unrolled loop of ADC operations.
Subtraction
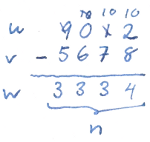
The subtraction algorithm is very similar to that for addition, except of course that it subtracts numbers instead of adding them, and overflow results in "borrows" instead of carries.
Another difference is that the first operand must be greater or equal to the second to ensure a non-negative result. A helper function is used to check this (it will be useful to have later as well).
/* Compare u with v, returning -1 if u < v, 1 if u > v, and 0 otherwise. */
static int cmp(int u_len, const uint32_t *u, int v_len, const uint32_t *v)
{
int i;
if (u_len != v_len) {
return u_len < v_len ? -1 : 1;
}
for (i = u_len - 1; i >= 0; i--) {
if (u[i] != v[i]) {
return u[i] < v[i] ? -1 : 1;
}
}
return 0;
}
/* Compute w = u - v, where u, v, w are n-place integers, and u >= v. */
static void algorithm_s(int n, const uint32_t *u, const uint32_t *v,
uint32_t *w)
{
bool borrow, borrow_a, borrow_b;
uint32_t diff_a, diff_b;
int j;
assert(cmp(n, u, n, v) >= 0 && "Subtraction result would be negative!");
borrow = false;
for (j = 0; j < n; j++) {
diff_a = u[j] - borrow;
borrow_a = (diff_a > u[j]);
diff_b = diff_a - v[j];
borrow_b = (diff_b > diff_a);
w[j] = diff_b;
assert(borrow_a + borrow_b <= 1);
borrow = borrow_a + borrow_b;
}
assert(!borrow && "Nothing to borrow from!");
}
Multiplication
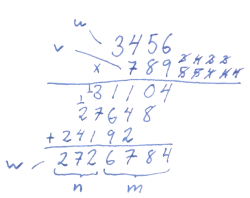
Multiplication requires a little more work than the two previous algorithms. The multiplicand is multiplied by one position of the multiplier at a time, and the intermediate results are added together. In school we would typically do the addition afterwards, but in this algorithm the results are accumulated as we go along.
The result of multiplying two 32-bit numbers requires up to 64 bits. This is normally not a problem even on 32-bit machines, which typically have a multiplication instruction that puts the result in two 32-bit registers. We will use a helper function for this.
/*
Multiply 32-bit numbers x and y into 64-bit (z_hi:z_lo).
This maps to a single instruction on most 32-bit CPUs,
including x86 and ARM.
*/
static void mul_32_by_32(uint32_t x, uint32_t y,
uint32_t *z_hi, uint32_t *z_lo)
{
uint64_t prod;
prod = (uint64_t)x * y;
*z_hi = (uint32_t)(prod >> 32);
*z_lo = (uint32_t)prod;
}
/* Multiply m-place u with n-place v, yielding (m + n)-place w. */
static void algorithm_m(int m, int n, const uint32_t *u, const uint32_t *v,
uint32_t *w)
{
int i, j;
uint32_t k, hi_prod, lo_prod;
bool carry_a, carry_b;
for (i = 0; i < m; i++) {
w[i] = 0;
}
for (j = 0; j < n; j++) {
if (v[j] == 0) {
w[j + m] = 0;
continue;
}
k = 0;
for (i = 0; i < m; i++) {
mul_32_by_32(u[i], v[j], &hi_prod, &lo_prod);
lo_prod += k;
carry_a = (lo_prod < k);
w[i + j] += lo_prod;
carry_b = (w[i + j] < lo_prod);
k = hi_prod + carry_a + carry_b;
assert(k >= hi_prod && "k cannot overflow");
}
w[j + m] = k;
}
}
While the previous algorithms were both of O(n) time complexity, this one is O(m*n). There are more advanced algorithms with lower time complexity that perform better for larger numbers; see for example the GMP manual chapter on multiplication algorithms.
Division
Division is the most complicated of the four basic operations, both in terms of the algorithm, and in terms of bookkeeping around our implementation.
The main snag is that the algorithm relies on an operation that divides a two-place integer by a one-place integer, resulting in a one-place quotient. X86's DIV instruction does precisely this, but it yields an exception on overflow (when the quotient is too large), and the compiler will therefore not use it with two-word divisors. Instead, we will implement the algorithm in terms of 16-bit numbers. The implementation in Hacker's Delight and LLVM's APInt class use the same approach, for example. (An alternative approach would be to use inline assembly to get the DIV instruction, and check the inputs to detect overflow. Another way would be to use multiplication by the reciprocal; see for example Niels Möller and Torbjörn Granlund "Improved division by invariant integers".)
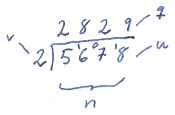
In the special case of a one-place dividend, the much simpler short division is performed instead. Each position of the divisor, right-to-left, is divided by the dividend, yielding one place of the result. The remainder of each operation is carried into the high word of the next division.
/* Divide (u_hi:u:lo) by v, setting q and r to the quotient and remainder. */
static void div_32_by_16(uint16_t u_hi, uint16_t u_lo, uint16_t v,
uint16_t *q, uint16_t *r)
{
uint32_t u = ((uint32_t)u_hi << 16) | u_lo;
assert(v > 0 && "Division by zero!");
assert(u / v <= UINT16_MAX && "Division overflow!");
*q = (uint16_t)(u / v);
*r = (uint16_t)(u % v);
}
/* Divide n-place u by v, yielding n-place quotient q and scalar remainder r. */
static void short_division(int n, uint16_t *u, uint16_t v,
uint16_t *q, uint16_t *r)
{
uint16_t k;
int i;
assert(v > 0 && "Division by zero!");
assert(n > 0 && "Dividing empty number!");
k = 0;
for (i = n - 1; i >= 0; i--) {
div_32_by_16(k, u[i], v, &q[i], &k);
}
*r = k;
}
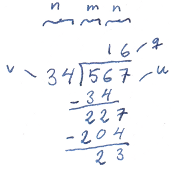
Below, we implement the long division algorithm, with helper functions used for the normalization step.
The normalization step multiplies u and v by a power of two (using bit shifts), such that the most significant bit in v is set. This ensures that the trial quotient, qhat, below is never too far off (see Knuth for details).
The result is computed one digit at a time by dividing u[0..n+j] by v[0..n-1] and subtracting the quotient multiplied by v from u. Since the operands are too large for the quotient to be computed directly, it is estimated as qhat instead (see Knuth for details.)
/* Count leading zeros in x. x must not be zero. */
static int leading_zeros(uint16_t x)
{
int n;
assert(x != 0);
n = 0;
while (x <= UINT16_MAX / 2) {
x <<= 1;
n++;
}
return n;
}
/* Shift n-place u m positions to the left. */
static void shift_left(int n, uint16_t *u, int m)
{
uint16_t k, t;
int i;
assert(m > 0);
assert(m < 16);
k = 0;
for (i = 0; i < n; i++) {
t = u[i] >> (16 - m);
u[i] = (u[i] << m) | k;
k = t;
}
assert(k == 0 && "Leftover carry!");
}
/* Shift n-place u m positions to the right. */
static void shift_right(int n, uint16_t *u, int m)
{
uint16_t k, t;
int i;
assert(m > 0);
assert(m < 16);
k = 0;
for (i = n - 1; i >= 0; i--) {
t = u[i] << (16 - m);
u[i] = (u[i] >> m) | k;
k = t;
}
assert(k == 0 && "Leftover carry!");
}
/*
Divide (m + n)-place u by n-place v, yielding (m + 1)-place quotient q and
n-place remainder u. u must have room for an (m + n + 1)th element.
*/
static void algorithm_d(int m, int n, uint16_t *u, uint16_t *v, uint16_t *q)
{
int shift;
int j, i;
uint32_t qhat, rhat, p, t;
uint16_t k, k2, d;
assert(n > 0 && "v must be greater than zero!");
assert(v[n - 1] != 0 && "v must not have leading zeros!");
if (n == 1) {
short_division(m + n, u, v[0], q, &u[0]);
return;
}
/* Normalize. */
u[m + n] = 0;
shift = leading_zeros(v[n-1]);
if (shift) {
shift_left(n, v, shift);
shift_left(m + n + 1, u, shift);
}
for (j = m; j >= 0; j--) {
/* Calculate qhat. */
t = ((uint32_t)u[j + n] << 16) | u[j + n - 1];
qhat = t / v[n - 1];
rhat = t % v[n - 1];
while (true) {
assert(n >= 2);
if (qhat > UINT16_MAX ||
qhat * v[n - 2] > ((rhat << 16) | u[j + n - 2])) {
qhat--;
rhat += v[n - 1];
if (rhat <= UINT16_MAX) {
continue;
}
}
break;
}
/* Multiply and subtract. */
k = 0;
for (i = 0; i <= n; i++) {
p = qhat * (i == n ? 0 : v[i]);
k2 = (p >> 16);
d = u[j + i] - (uint16_t)p;
k2 += (d > u[j + i]);
u[j + i] = d - k;
k2 += (u[j + i] > d);
k = k2;
}
/* Test remainder. */
q[j] = qhat;
if (k != 0) {
/* Add back. */
q[j]--;
k = 0;
for (i = 0; i < n; i++) {
t = u[j + i] + v[i] + k;
u[j + i] = (uint16_t)t;
k = t >> 16;
}
u[j + n] += k;
}
}
/* Unnormalize. */
if (shift) {
shift_right(n, u, shift);
}
}
As with multiplication, there are more advanced algorithms with better time complexity; see for example the GMP manual chapter on division algorithms.
To be able to divide 32-bit numbers, we use the functions below for converting between 32- and 16-bit numbers.
/* Copy n uint32_t values from u32 to u16. */
static void u32_to_u16(int n, const uint32_t *u32, uint16_t *u16)
{
int i;
for (i = 0; i < n; i++) {
u16[i * 2 + 0] = (uint16_t)u32[i];
u16[i * 2 + 1] = (uint16_t)(u32[i] >> 16);
}
}
/* Copy n uint16_t values from u16 to u32. */
static void u16_to_u32(int n, const uint16_t *u16, uint32_t *u32)
{
int i;
assert((n % 2) == 0 && "Expected n to be even!");
for (i = 0; i < n; i += 2) {
u32[i / 2] = u16[i] | ((uint32_t)u16[i + 1] << 16);
}
}
/*
Divide (m + n)-place u with n-place v, yielding (m + 1)-place quotient q and
n-place remainder r.
*/
static void algorithm_d_wrapper(int m, int n, const uint32_t *u,
const uint32_t *v, uint32_t *q, uint32_t *r)
{
/* To avoid having to do 64-bit divisions, convert to uint16_t. Also
extend the dividend one place, as that is required for the
normalization step. */
uint16_t u16[(m + n) * 2 + 1];
uint16_t v16[n * 2];
uint16_t q16[(m + 1) * 2];
bool v_zero;
assert(n > 0 && "Division by zero!");
assert(v[n - 1] != 0 && "v has leading zero!");
u32_to_u16(m + n, u, u16);
u32_to_u16(n, v, v16);
/* If v16 has a leading zero, treat it as one place shorter. */
v_zero = (v16[n * 2 - 1] == 0);
algorithm_d(m * 2 + v_zero, n * 2 - v_zero, u16, v16, q16);
if (v_zero) {
/* If v16 was short, pad the remainder. */
u16[n * 2 - 1] = 0;
} else {
/* Pad the quotient. */
q16[(m + 1) * 2 - 1] = 0;
}
u16_to_u32((m + 1) * 2, q16, q);
u16_to_u32(n * 2, u16, r);
}
String Conversions
The functions below convert between human-readable representations (strings of decimal characters) and uint32_t arrays that the algorithms above use.
Decimal strings are converted in chunks of up to 9 characters at a time, to make sure each chunk fits in an uint32_t. Each chunk is then added to the current number multiplied by 10^x where x is the number of characters in the chunk.
/* Multiply m-place integer u by x and add y to it; set m to the new size. */
static void multiply_add(uint32_t *u, int *m, uint32_t x, uint32_t y)
{
int i;
uint32_t k, hi_prod, lo_prod;
k = y;
for (i = 0; i < *m; i++) {
mul_32_by_32(u[i], x, &hi_prod, &lo_prod);
lo_prod += k;
k = hi_prod + (lo_prod < k);
u[i] = lo_prod;
}
if (k) {
u[*m] = k;
(*m)++;
}
}
/* Convert n-character decimal string str into integer u. */
static void from_string(int n, const char *str, int *u_len, uint32_t *u)
{
uint32_t chunk;
int i;
static const uint32_t pow10s[] = {1000000000,
10,
100,
1000,
10000,
100000,
1000000,
10000000,
100000000};
*u_len = 0;
chunk = 0;
/* Process the string in chunks of up to 9 characters, as 10**9 is the
largest power of 10 that fits in uint32_t. */
for (i = 1; i <= n; i++) {
assert(*str >= '0' && *str <= '9');
chunk = chunk * 10 + *str++ - '0';
if (i % 9 == 0 || i == n) {
multiply_add(u, u_len, pow10s[i % 9], chunk);
chunk = 0;
}
}
}
Turning a number into a decimal string is usually done by dividing it by 10 to extract the least significant decimal digit as the remainder, and repeating until the number reaches zero.
The same idea is used to turn our integers to strings, except the divisions are more expensive so we divide by a larger power of 10 to extract several digits at once. As in the division algorithm above, we convert to uint16_t first.
/* Turn n-place integer u into decimal string str. */
static void to_string(int n, const uint32_t *u, char *str)
{
uint16_t v[n * 2];
uint16_t k;
char *s, t;
int i;
/* Make a scratch copy that's easy to do division on. */
u32_to_u16(n, u, v);
n *= 2;
/* Skip leading zeros. */
while (n && v[n - 1] == 0) {
n--;
}
/* Special case for zero to avoid generating an empty string. */
if (n == 0) {
str[0] = '0';
str[1] = '\0';
return;
}
s = str;
while (n != 0) {
/* Divide by 10**4 to get the 4 least significant decimals. */
short_division(n, v, 10000, v, &k);
/* Skip leading zeros. */
while (n && v[n - 1] == 0) {
n--;
}
/* Add the digits to the string in reverse, with padding unless
this is the most significant group of digits (n == 0). */
for (i = 0; (n != 0 && i < 4) || k; i++) {
*s++ = '0' + (k % 10);
k /= 10;
}
}
/* Terminate and reverse the string. */
*s-- = '\0';
while (str < s) {
t = *str;
*str++ = *s;
*s-- = t;
}
}
The bigint Interface
The low-level functions above are not very user-friendly. Rather than using them directly, we will use them to implement the more high-level interface below. In addition to being much easier to use, it also supports signed integers.
Note that the functions are still fairly low-level in the sense that they will not handle, for example, division by zero, or malformed decimal strings.
typedef struct bigint_t bigint_t;
/* Create a bigint from n-length array u. Leading zeros or n = 0 are allowed. */
bigint_t *bigint_create(int n, const uint32_t *u, bool negative);
/* Create a bigint from n-character string str, consisting of one or more
decimal characters, with an optional preceding hyphen. */
bigint_t *bigint_create_str(int n, const char *str);
/* Get the maximum required string length for x. */
size_t bigint_max_stringlen(const bigint_t *x);
/* Convert bigint to decimal string. */
void bigint_tostring(const bigint_t *x, char *str);
/* Print a bigint to stdout in decimal. */
void bigint_print(const bigint_t *x);
/* Arithmetic. Division does truncation towards zero, and the remainder will
have the same sign as the divisor. Division by zero is not allowed. */
bigint_t *bigint_add(const bigint_t *x, const bigint_t *y);
bigint_t *bigint_sub(const bigint_t *x, const bigint_t *y);
bigint_t *bigint_mul(const bigint_t *x, const bigint_t *y);
bigint_t *bigint_div(const bigint_t *x, const bigint_t *y);
bigint_t *bigint_rem(const bigint_t *x, const bigint_t *y);
bigint_t *bigint_neg(const bigint_t *x);
/* Comparison: returns -1 if x < y, 1 if x > y, and 0 if they are equal. */
int bigint_cmp(const bigint_t *x, const bigint_t *y);
/* Check whether x is zero. */
bool bigint_is_zero(const bigint_t *x);
Note that in this interface, bigint objects are immutable. In many applications, it would be more efficient to allow, for example, adding a number to an existing bigint without creating a new object.
A bigint_t is implemented by this type:
struct bigint_t {
uint32_t length : 31;
uint32_t negative : 1;
uint32_t data[];
};
The functions below create bigint_t objects:
bigint_t *bigint_create(int n, const uint32_t *u, bool negative)
{
bigint_t *res;
/* Strip leading zeros. A bigint_t will never contain leading zeros. */
while (n > 0 && u[n - 1] == 0) {
n--;
}
res = malloc(sizeof(*res) + n * sizeof(uint32_t));
if (res == NULL) {
fprintf(stderr, "Out of memory!");
exit(1);
}
res->length = n;
if (n == 0) {
res->negative = false;
} else {
res->negative = negative;
memcpy(res->data, u, sizeof(res->data[0]) * n);
}
return res;
}
bigint_t *bigint_create_str(int n, const char *str)
{
uint32_t u[n / 9 + 1]; /* A uint32_t holds at least 9 decimals. */
bool negative = false;
int u_length;
assert(n > 0 && "Empty string is not a valid number.");
if (str[0] == '-') {
assert(n > 1 && "Just '-' is not a valid number.");
negative = true;
str++;
n--;
}
from_string(n, str, &u_length, u);
return bigint_create(u_length, u, negative);
}
Functions for converting to a string and printing:
size_t bigint_max_stringlen(const bigint_t *x)
{
if (x->length == 0) {
return 1;
}
/* 10 digits per uint32_t, one more for '-'. */
return x->length * 10 + x->negative;
}
void bigint_tostring(const bigint_t *x, char *str)
{
if (x->negative) {
*str++ = '-';
}
to_string(x->length, x->data, str);
assert(strlen(str) <= bigint_max_stringlen(x));
}
void bigint_print(const bigint_t *x)
{
char str[bigint_max_stringlen(x) + 1];
bigint_tostring(x, str);
puts(str);
}
The low-level functions for addition and subtraction require the operands to be of the same size, and in the case of subtraction that one of them (the minuend) is greater or equal to the other. The function below deal with all of that, as well as signs, to implement subtraction and addition of bigints:
static bigint_t *add(int x_len, const uint32_t *x, int y_len, const uint32_t *y)
{
if (x_len < y_len) {
return add(y_len, y, x_len, x);
}
int w_len = x_len + 1;
uint32_t w[w_len];
int i;
assert(x_len >= y_len);
/* Copy y into w, and pad it to the same length as x. */
for (i = 0; i < y_len; i++) {
w[i] = y[i];
}
for (i = y_len; i < x_len; i++) {
w[i] = 0;
}
/* w = x + w */
algorithm_a(x_len, x, w, w);
return bigint_create(w_len, w, false);
}
static bigint_t *sub(int x_len, const uint32_t *x, int y_len, const uint32_t *y)
{
bigint_t *z;
if (cmp(x_len, x, y_len, y) < 0) {
/* x - y = -(y - x) */
z = sub(y_len, y, x_len, x);
z->negative = true;
return z;
}
uint32_t w[x_len];
int i;
assert(x_len >= y_len);
/* Copy y into w, and pad to the same length as x. */
for (i = 0; i < y_len; i++) {
w[i] = y[i];
}
for (i = y_len; i < x_len; i++) {
w[i] = 0;
}
/* w = x - w */
algorithm_s(x_len, x, w, w);
return bigint_create(x_len, w, false);
}
bigint_t *bigint_add(const bigint_t *x, const bigint_t *y)
{
bigint_t *z;
if (x->negative && y->negative) {
/* (-x) + (-y) = -(x + y) */
z = add(x->length, x->data, y->length, y->data);
z->negative = true;
return z;
}
if (x->negative) {
assert(!y->negative);
/* (-x) + y = y - x */
return sub(y->length, y->data, x->length, x->data);
}
if (y->negative) {
assert(!x->negative);
/* x + (-y) = x - y */
return sub(x->length, x->data, y->length, y->data);
}
assert(!x->negative && !y->negative);
return add(x->length, x->data, y->length, y->data);
}
bigint_t *bigint_sub(const bigint_t *x, const bigint_t *y)
{
bigint_t *z;
if (x->negative && y->negative) {
/* (-x) - (-y) = y - x */
return sub(y->length, y->data, x->length, x->data);
}
if (x->negative) {
assert(!y->negative);
/* (-x) - y = -(x + y) */
z = add(x->length, x->data, y->length, y->data);
z->negative = true;
return z;
}
if (y->negative) {
assert(!x->negative);
/* x - (-y) = x + y */
return add(x->length, x->data, y->length, y->data);
}
assert(!x->negative && !y->negative);
return sub(x->length, x->data, y->length, y->data);
}
For multiplication and division, dealing with the signs requires less work:
bigint_t *bigint_mul(const bigint_t *x, const bigint_t *y)
{
uint32_t w[x->length + y->length];
algorithm_m(x->length, y->length, x->data, y->data, w);
return bigint_create(x->length + y->length, w,
x->negative ^ y->negative);
}
static bigint_t *divrem(int x_len, const uint32_t *x,
int y_len, const uint32_t *y,
bool remainder)
{
uint32_t q[x_len - y_len + 1];
uint32_t r[y_len];
assert(x_len >= y_len);
algorithm_d_wrapper(x_len - y_len, y_len, x, y, q, r);
if (remainder) {
return bigint_create(y_len, r, false);
}
return bigint_create(x_len - y_len + 1, q, false);
}
bigint_t *bigint_div(const bigint_t *x, const bigint_t *y)
{
bigint_t *z;
if (x->length < y->length) {
return bigint_create(0, NULL, false);
}
z = divrem(x->length, x->data, y->length, y->data, false);
z->negative = x->negative ^ y->negative;
return z;
}
bigint_t *bigint_rem(const bigint_t *x, const bigint_t *y)
{
bigint_t *z;
if (x->length < y->length) {
z = bigint_create(x->length, x->data, false);
} else {
z = divrem(x->length, x->data, y->length, y->data, true);
}
z->negative = x->negative;
return z;
}
Finally, these functions complete the implementation of the interface:
bigint_t *bigint_neg(const bigint_t *x)
{
return bigint_create(x->length, x->data, x->negative ^ 1);
}
int bigint_cmp(const bigint_t *x, const bigint_t *y)
{
if (x->negative != y->negative) {
return x->negative ? -1 : 1;
}
assert(x->negative == y->negative);
if (x->negative) {
return cmp(y->length, y->data, x->length, x->data);
}
return cmp(x->length, x->data, y->length, y->data);
}
bool bigint_is_zero(const bigint_t *x)
{
return x->length == 0;
}
The Calculator
The calculator consists of a simple lexer which breaks the input into tokens that are then consumed by a recursive descent parser. The parser evaluates the expressions as they are parsed.
enum token_kind { ADD, SUB, MUL, DIV, LP, RP, NUM, EOL, END };
struct token_t {
enum token_kind kind;
bigint_t *value;
};
static struct token_t current_token;
static void error(const char *msg, ...)
{
va_list ap;
va_start(ap, msg);
fputs("error: ", stderr);
vfprintf(stderr, msg, ap);
fputc('\n', stderr);
va_end(ap);
exit(1);
}
#define BUFFER_SIZE (100*1024)
static char buffer[BUFFER_SIZE];
static void next_token(void)
{
int c;
size_t len;
assert(current_token.kind != END && "Can't get token after END!");
do {
c = getchar();
} while (c == ' ' || c == '\t');
switch (c) {
case '+':
current_token.kind = ADD;
return;
case '-':
current_token.kind = SUB;
return;
case '*':
current_token.kind = MUL;
return;
case '/':
current_token.kind = DIV;
return;
case '(':
current_token.kind = LP;
return;
case ')':
current_token.kind = RP;
return;
case '\n':
current_token.kind = EOL;
return;
case EOF:
current_token.kind = END;
return;
}
len = 0;
while (c >= '0' && c <= '9') {
if (len == BUFFER_SIZE) {
error("number too long!");
}
buffer[len++] = c;
c = getchar();
}
if (len > 0) {
ungetc(c, stdin);
current_token.kind = NUM;
current_token.value = bigint_create_str(len, buffer);
return;
}
error("unexpected character: '%c'", c);
}
/*
Grammar:
<expr> ::= <sum> EOL | END
<sum> ::= <term> (ADD <term> | SUB <term>)*
<term> ::= <factor> (MUL <factor> | DIV <factor>)*
<factor> ::= SUB <factor> | LP <sum> RP | <number>
The functions below parse a string of tokens according to the grammar and
return the corresponding bigint value. expr() leaves the last token
unconsumed to avoid blocking on input.
*/
static bigint_t *expr(void);
static bigint_t *sum(void);
static bigint_t *term(void);
static bigint_t *factor(void);
static bigint_t *expr(void)
{
bigint_t *res;
if (current_token.kind == END) {
return NULL;
}
res = sum();
if (current_token.kind != EOL) {
error("trailing character(s)");
}
return res;
}
static bigint_t *sum(void)
{
bigint_t *x, *y, *t;
x = term();
while (true) {
if (current_token.kind == ADD) {
next_token();
y = term();
t = bigint_add(x, y);
free(x);
free(y);
x = t;
} else if (current_token.kind == SUB) {
next_token();
y = term();
t = bigint_sub(x, y);
free(x);
free(y);
x = t;
} else {
break;
}
}
return x;
}
static bigint_t *term(void)
{
bigint_t *x, *y, *t;
x = factor();
while (true) {
if (current_token.kind == MUL) {
next_token();
y = factor();
t = bigint_mul(x, y);
free(x);
free(y);
x = t;
} else if (current_token.kind == DIV) {
next_token();
y = factor();
if (bigint_is_zero(y)) {
error("division by zero!");
}
t = bigint_div(x, y);
free(x);
free(y);
x = t;
} else {
break;
}
}
return x;
}
static bigint_t *factor(void)
{
bigint_t *x, *res;
if (current_token.kind == SUB) {
next_token();
x = factor();
res = bigint_neg(x);
free(x);
} else if (current_token.kind == LP) {
next_token();
res = sum();
if (current_token.kind != RP) {
error("expected ')'");
}
next_token();
} else if (current_token.kind == NUM) {
res = current_token.value;
next_token();
} else {
error("expected '-', number or '('");
}
return res;
}
int main()
{
bigint_t *x;
for (;;) {
next_token();
x = expr();
if (x == NULL) {
break;
}
bigint_print(x);
free(x);
printf("\n");
}
return 0;
}
Demo
The full code is available in bigint.h, bigint.c, and calc.c.
Compiling and testing the calculator on Linux or Mac OS X:
$ gcc calc.c bigint.c -o calc
$ ./calc
-934834834934583458 * (847467494749 - 9364617634234234234234) / (1 + 123456789123456)
70910403888588273104107053
Hopefully the result is correct :-)