
Green's Sorting Network
and a Cheque From Knuth
(2 April 2016)
The first time I heard about Don Knuth and his famous books, The Art of Computer Programming (TAOCP), was during a summer internship more than ten years ago. When my colleague explained how Knuth pays a finder's fee for any errors in his books, cheques more commonly framed than cashed, I hardly expected to ever receive one myself.
The Sorting Network
These events started with John Regehr's Nibble Sort Contest about a year ago. The fastest solution (explained here) uses a sorting network, specifically this one:
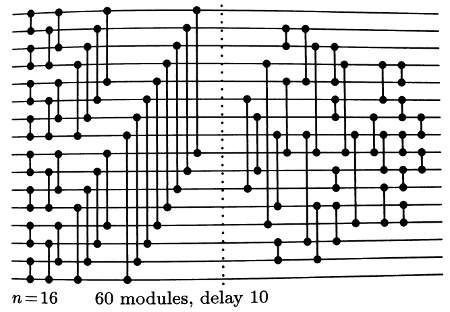
(See for example this chapter from Introduction to Algorithms for information on sorting networks.)
This network can be found in TAOCP Section 5.3.4 (Vol 3, page 227), where Knuth describes its history:
"A 62-comparator sorting network for 16 elements was found by G. Shapiro in 1969, and this was rather surprising since Batcher's method (63 comparisons) would appear to be at its best when n is a power of 2. Soon after hearing of Shapiro's construction, M. W. Green tripled the amount of surprise by finding the 60-comparison sorter in Fig. 49."
Surprising indeed! How did Green come up with this network?
Green's Paper
I found articles referencing a paper by Green: "Some improvements in nonadaptive sorting algorithms" in Proceedings of the Sixth Annual Princeton Conference on Information Sciences and Systems, pages 387–391, 1972. Would that have the explanation?
It turned out that this paper is impossible to find online. I tried to check local univeristy libraries for a copy of the proceedings, but the WorldCat entry says the nearest copy is in Denver, Colorado, which would be a long trip for me.
I then had the idea of emailing authors of more recent articles which reference Green's paper; surely they must have read it, and maybe they could give me a copy. I had only sent two emails when one author got back to me and said he couldn't provide a copy, but he did point out that the physical proceedings were available at on-line used bookstores!
Eventually, the volume arrived:

Reading the paper was a bit of a disappointment. Green explains how the "front part" of the network (the comparators before the dotted line in the figure) is constructed, calling it an orthogonal network. However, the paper does not show the remaining 28 comparators, nor does it explain how they were found:
"For the case p = 4, where the orthogonal network has 16 inputs, there are 168 output vectors. The structure of these vectors is sufficiently complex that it takes some ingenuity to find a minimal set of cells that will resolve the residual ambiguities. We believe that 28 cells are necessary, leading to a 16-sorter with 32 + 28 = 60 cells. The latter 60-cell network (whose correctness has been verified by a computer program) contains three fewer cells than Batcher's 16-sorter."
Emailing Knuth
Since Knuth includes Green's network in his book, maybe he would have some more information about this network and how Green came up with it. And even though Green's paper doesn't provide a full explanation for the network, perhaps it should still be referenced in the text?
I emailed Knuth on the evening of 15 December. Two days later, I received a message from his secretary, asking to confirm my postal address as Knuth had a reply for me. She said the reply would go out with the post that day.
Then followed a long wait, with unusually frequent checking of the mail.
Mid-January, I wrote to ask about the status of the letter. The secretary confirmed that the letter had been sent on 18 December, and there was no way to track it.
A few hours later, I received another email from a mysterious address:
Dear Hans,
Maybe that letter was lost in the mail --- however, the US Postal Service tends to get behind at that time of year, and Stanford also closes down for two or three weeks! So there still is hope.
I don't recall what I wrote, but I think it basically said that I happen to own Jeff Ullman's former copies of those Princeton symposia, and I had read the issue but didn't flag Mike Green's paper at the time. Now I've add a reference to it in the answer to exercise 5.3.4--32, and I also wrote a "check" for $2.56 as a thank-you for the omission. [See http://www-cs-faculty.stanford.edu/~knuth/boss.html for your account info.]
If another month goes by and you still haven't received the check, I can send a replacement (although neither is actually "negotiable"!). But I doubt if I can reproduce anything else that I might have written in my reply --- I have dozens of these things going out the door all the time. My files don't contain any other hints of how he came up with his network.
Happy 2016 to you! -- Don Knuth
This made me very happy (and considering his email policy, perhaps an email from Knuth is even more rare than a cheque?).
Another month went by, and the replacement cheque arrived:
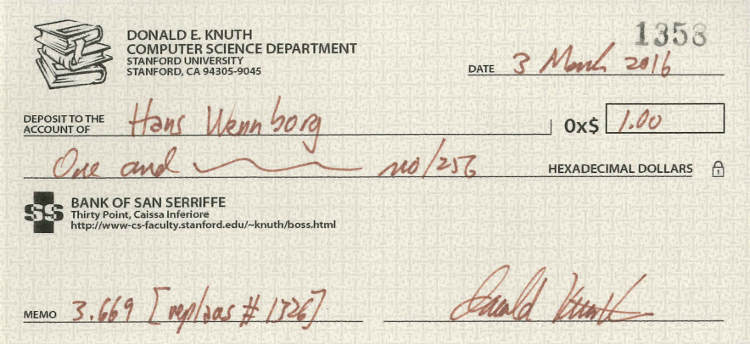
It is now sitting in a frame, acting kind of as a substitute for the Ph.D. diploma I never pursued.
As for Green's sorting network, the mystery still remains: how was the network constructed? If I understand correctly, no one has been able to reproduce the same network since, and only more recently were other networks of the same size discovered (see Hugues Juillé's web page). With more ingenuity and 21st century computational power, is it possible to find a smaller network?
Update 2021-05-13: Jannis Harder has an interesting blog post about proving the optimality of Shapiro and Green's 11- and 12-element sorting networks.