
Zip Files:
History, Explanation and Implementation
(26 February 2020)
I have been curious about data compression and the Zip file format in particular for a long time. At some point I decided to address that by learning how it works and writing my own Zip program. The implementation turned into an exciting programming exercise; there is great pleasure to be had from creating a well oiled machine that takes data apart, jumbles its bits into a more efficient representation, and puts it all back together again. Hopefully it is interesting to read about too.
This article explains how the Zip file format and its compression scheme work in great detail: LZ77 compression, Huffman coding, Deflate and all. It tells some of the history, and provides a reasonably efficient example implementation written from scratch in C. The source code is available in hwzip-2.4.zip.
I have done my best to provide a bug-free implementation. If you find any issues, please let me know.
I am very grateful to Ange Albertini, Gynvael Coldwind, Fabian Giesen, Jonas Skeppstedt (web), Primiano Tucci, and Nico Weber who provided valuable feedback on draft versions of this material.
Update 2024-09-01: Tweak how compute_huffman_lengths limits the Huffman code lengths. The change is part of hwzip-2.4.zip.
Update 2023-06-10: Added a paragraph about how Info-Zip's zip and unzip programs, as well as gzip, could support Deflate before PKZip 2.04 had been released. Updated ctime2dos() to avoid converting dates outside the supported range. That change is part of hwzip-2.2.zip.
Update 2022-04-30: Hadrien Dorio ported hwzip to the Zig programming language. In the process he found an overflow bug in the compression ratio computation in zip_callback() and some incorrect uses of the CHECK macro in the unit tests. Those bugs have been fixed in hwzip-2.1.zip.
Update 2021-03-12: I wrote a follow-up article about the legacy Zip compression methods: Shrink, Reduce, and Implode. The code is in hwzip-2.0.zip.
Update 2020-10-11: In hwzip-1.4.zip, the distance2dist table was split into two smaller tables, reducing the binary size by 32 KB. It also ensures that Deflate blocks always emit at least two non-zero dist codeword lengths, for compatibility with old Zlib versions.
Update 2020-06-14: In hwzip-1.3.zip, the minimum Lempel–Ziv back reference length was increased from three to four bytes, and the hash was changed from a three-byte rolling hash to a four-byte multiplicative hash. This made Deflate compression more than twice as fast as the previous version.
Table of Contents
- History
- Lempel–Ziv Compression (LZ77)
- Huffman Coding
- Deflate
- The Zip File Format
- HWZip
- Conclusion
- Exercises
- Further Reading
- Linked Files
History
PKZip
Back in the eighties and early nineties, before the Internet became widely available, home computer enthusiasts used dial-up modems to connect to Bulletin Board Systems (BBSes) over the telephone network. A BBS is an interactive computer system that typically allows users to send messages, play games, and share files. All that was needed to go online was a computer, a modem, and the phone number of a good BBS—something that could be found in lists published by computer magazines, and on other BBSes.
One important tool for making file sharing easier was the archiver. An archiver stores one or more files into a single file, an archive, allowing the files to be stored or transferred as a single unit, and ideally also compresses them to save storage space and transfer time. One such archiver that was popular with the BBS scene was Arc, written by Thom Henderson of System Enhancement Associates (SEA), a small company he had founded with his brother-in-law.
In the late eighties, a programmer named Phil Katz released his own Arc program, PKArc. It was compatible with SEA's Arc, but faster due to routines written in assembly, and it had a new compression method added by Katz. The program became popular, and Katz quit his job and founded PKWare to focus on developing it. According to legend, much of the work took place at his mother Hildegard's kitchen table in Glendale, Wisconsin.

Phil Katz (1962–2000). Photo from an article in the Milwaukee Sentinel, 19 September 1994.
SEA, however, were not thrilled by Katz's initiative. They sued for trademark violation and copyright infringement. The dispute and the surrounding debate in the BBS and PC world became known as the Arc Wars. In the end, the case was settled to SEA's advantage.
Moving on from Arc, in 1989 Katz created a new archive format which he named Zip and dedicated to the public domain:
The file format of the files created by these programs, which file format is original with the first release of this software, is hereby dedicated to the public domain. Further, the filename extension of ".ZIP", first used in connection with data compression software on the first release of this software, is also hereby dedicated to the public domain, with the fervent and sincere hope that it will not be attempted to be appropriated by anyone else for their exclusive use, but rather that it will be used to refer to data compression and librarying software in general, of a class or type which creates files having a format generally compatible with this software.
Katz's program for creating such files was called PKZip, and it was soon adopted by the BBS and PC world.
One aspect that most likely contributed to the Zip format's success was that PKZip came with a document, the Application Note, which explained exactly how the format works. This allowed others to study the format and create programs that create, extract, or otherwise interact with Zip files in a compatible way.
Zip is a lossless compression format: after decompression, the data is identical to what it was before compression. It works by finding redundancies in the source data and representing it more efficiently. This is different from lossy compression, used in image and sound formats such as JPEG and MP3, which work by removing features from the data which are less perceivable to the human eye or ear, etc.
PKZip was distributed as Shareware: it could be used and copied freely, but users were encouraged to "register" the program. For $47, one would receive a printed manual, premium support, and an enhanced version of the software.

The seminal version of PKZip was 2.04c, from 28 December 1992, soon followed by bug fix release 2.04g. This introduced Deflate as the default compression method, and defined how Zip file compression would work going forward. (Boardwatch article about the release.)
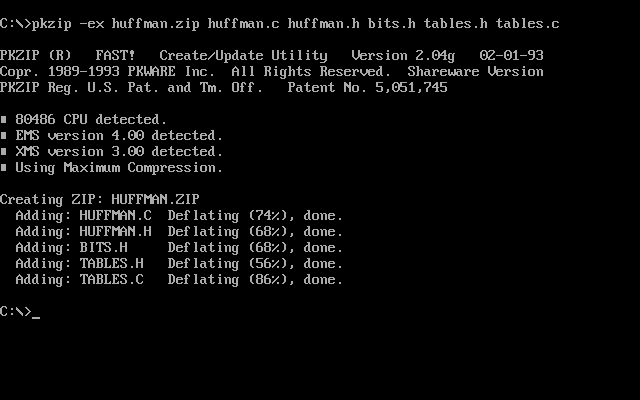
The Zip format has since been adopted by many other file formats. For example, Java Archives (.jar files) and Android Application Packages (.apk files), as well as Microsoft Office .docx files, are all using the Zip format. Other file formats and protocols re-use the compression algorithm used in Zip files, Deflate. For example, this web page was most likely transferred to your web browser as a gzip file, a format which uses Deflate compression.
Phil Katz passed away in 2000. PKWare still exist and maintain the Zip format, though they focus mainly on data security software.
Info-Zip and Zlib
Soon after the release of PKZip in 1989, other programs to extract Zip files started showing up, in particular a program called unzip that could be used to extract Zip files on Unix systems. A mailing list called Info-Zip was set up in March 1990.
The Info-Zip group released the free and open-source unzip and zip programs, used to extract and create zip files. The code was ported to many systems and they are still the standard Zip programs used on Unix systems. This further helped increase the popularity of Zip files.
Although the Deflate compression method was first officially released with PKZip 2.04 in December 1992, it had been available in PKZip "alpha release" pkz193a.exe since October 1991. Based on that, Info-Zip added support for the new compression method to their programs, and officially released zip and unzip with Deflate support already in August 1992. This also explains how gzip could use Deflate compression, although its first release (October 1992 according to the changelog) predates PKZip 2.04.
At some point, the Info-Zip code that performed the Deflate compression and decompression was extracted into a separate software library called Zlib, written by Jean-loup Gailly (compression) and Mark Adler (decompression).

Jean-loup Gailly (left) and Mark Adler (right) receiving the USENIX STUG Award in 2009.
One reason for creating the library was that this made it convenient to use Deflate compression in other applications and file formats, such as the new gzip file compression format, and the PNG image compression format. These new file formats had been proposed in order to replace the Compress and GIF file formats, which used the patent-encumbered LZW algorithm.
As part of developing those formats, a specification of Deflate was written by L Peter Deutsch and published as Internet RFC 1951 in May 1996. This provides an easier to follow description than the original PKZip Application Note.
Today, the use of Zlib is truly ubiquitous. It was probably responsible for both the compression of this page on the web server, and decompression in your web browser. Compression and decompression of most Zip and Zip-like files is now done with Zlib.
WinZip
Many people who did not use PKZip do remember using WinZip. As PC users moved from DOS to Windows, they also moved from PKZip to WinZip.
It started as a project by programmer Nico Mak, who was working on software for the OS/2 operating system at a company called Mansfield Software Group in Storrs-Mansfield, Connecticut. He was using Presentation Manager, the graphical user interface in OS/2, and was frustrated by how he had to switch from its File Manager to a DOS command prompt whenever he wanted to create or extract Zip files.
Mak wrote a simple graphical program to manage Zip files directly in Presentation Manager, named it PMZip, and released it as shareware in 1990.
OS/2 never really took off; instead the PC world was moving to Microsoft Windows. In 1991, Mak decided to learn how to write Windows programs, and his first project was to port his Zip program to this new operating system. WinZip 1.00 was released in April 1991 as shareware with a 21-day evaluation period and $29 registration price. It looked like this:
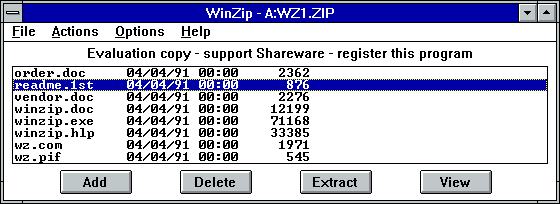
The first versions of WinZip used PKZip behind the scenes, but starting with version 5.0 in 1993 it uses the code from Info-Zip to manage Zip files directly. From its humble beginnings, the user interface evolved to different versions of the one below.
Screenshot of WinZip 6.3 running under Windows 3.11 for Workgroups.
WinZip was one of the most popular shareware programs during the nineties, but it eventually became less relevant as operating systems gained built-in support for Zip files. Windows manages Zip files as "compressed folders" since Windows ME (or Windows 98 with Plus! 98). The Windows integration was written by Dave Plummer and distributed as a shareware product before Microsoft acquired it. See Dave's video for the story.
Windows compressed folders use a library called DynaZip to manage Zip files under the hood. The library came about as Neil Rosenberg and Glen Horton at Inner Media needed a way to create Zip files in their screen capture/image management tool Collage. Based on an early version of Info-Zip, they built a Windows library which became very popular with developers.
Mak's company was originally called Nico Mak Computing. In 2000 it was renamed to WinZip Computing, and Mak seems to have left around this time. In 2005 the company was sold to Vector Capital, and it eventually ended up owned by Corel who still release WinZip as a product.
Lempel–Ziv Compression (LZ77)
There are two main ingredients in Zip compression: Lempel–Ziv compression and Huffman coding. This section describes the former.
One way of compressing text is to maintain a list of common words or phrases, and replace occurrences of those words in the text with references to the dictionary. For example, a long word such as "compression" in the original text might be represented more efficiently as #1234, where 1234 refers to the position in the word list. This is known as dictionary-based compression.
The dictionary method poses several problems for a general-purpose compression scheme. First, what should go in the dictionary? The original data might not be in English, and it might not even be human-readable text. And if the dictionary is not agreed upon between the compressing and decompressing parties beforehand, it needs to be stored and transmitted together with the compressed data, reducing the benefit of the compression.
One elegant solution to these problems is to use the original data itself as the dictionary. In their 1977 paper "A Universal Algorithm for Sequential Data Compression", Jacob Ziv and Abraham Lempel (both at Technion), propose a compression scheme where the original data is parsed into a sequence of triplets
(pointer, length, next)
where pointer and length form a back reference to a substring to be copied from a previous position in the original text, and next is the next character to output.


Abraham Lempel (1936–2023) and Jacob Ziv (1931–2023). Photos from Wikipedia (Staelin, CC BY 3.0) and Wikipedia.
For example, consider the snippet below.
It was the best of times,
it was the worst of times,
In the second line, the "t was the w" substring can be represented as (26, 10, w), because it can be recreated by copying 10 characters from the position 26 steps back, followed by a "w". Characters which have not occurred before use zero-length back references. For example, the initial "I" would be represented as (0, 0, I).
This form of compression is called Lempel–Ziv or LZ77 compression. However, real-world implementations typically do not use the next part of the triplets. Instead, they output single characters separately and use (distance, length) pairs for the back references. (This variant is called LZSS compression.) How the literals and back reference are encoded is a separate problem, and we will see how it is done in Deflate later.
As an example, the following text
It was the best of times,
it was the worst of times,
it was the age of wisdom,
it was the age of foolishness,
it was the epoch of belief,
it was the epoch of incredulity,
it was the season of Light,
it was the season of Darkness,
it was the spring of hope,
it was the winter of despair,
we had everything before us,
we had nothing before us,
we were all going direct to Heaven,
we were all going direct the other way
can be compressed into
It was the best of times, i(26,10)
wor(27,24)age(25,4)wisdom(26,20)
foolishnes(57,14)epoch(33,4)
belief(28,22)incredulity(33,13)
season(34,4)Light(28,23)Dark(120,17)
spring(31,4)hope(231,14)inter(27,4)
despair, we had everyth(57,4)before us(29,9)
no(26,20)were all go(29,4)
direct to Heaven(36,28)he other way
One exciting aspect of back references is that they can overlap with themselves, which happens when the length is greater than the distance. This is best illustrated by an example:
Fa-la-la-la-la
can be compressed into
Fa-la(3,9)
This may seem strange, but it works: once the first three "-la" bytes have been copied, the copying continues using the recently output bytes.
This is effectively a form of run-length encoding, where a piece of data is copied repeatedly up to a certain length.
See Colin Morris's Are Pop Lyrics Getting More Repetitive? article for an interactive example of Lempel–Ziv compression applied to song lyrics.
Expressed in C, a back reference can be copied out as shown below. Note that because of the possible self-overlap, we cannot use memcpy or memmove.
/* Output the (dist,len) back reference at dst_pos in dst. */
static inline void lz77_output_backref(uint8_t *dst, size_t dst_pos,
size_t dist, size_t len)
{
size_t i;
assert(dist <= dst_pos && "cannot reference before beginning of dst");
for (i = 0; i < len; i++) {
dst[dst_pos] = dst[dst_pos - dist];
dst_pos++;
}
}
Literals are trivial to output but we provide a utility function for completeness:
/* Output a literal byte at dst_pos in dst. */
static inline void lz77_output_lit(uint8_t *dst, size_t dst_pos, uint8_t lit)
{
dst[dst_pos] = lit;
}
Note that the caller of these functions is responsible for making sure there is enough room in dst for the output, and that the back reference does not try to go before the start of the buffer.
Of course the hard part is not to output back references during decompression, but rather how to find them in the first place when compressing the original data. There are different ways of doing that, but we will follow Zlib's hash table-based approach, which is also what RFC 1951 suggests.
The idea is to maintain a hash table with the positions of four-character prefixes that have occurred previously in the string (shorter back references are not considered profitable). For Deflate, only back references to the most recent 32,768 characters, the window, are allowed. This enables streaming compression: the input can be processed a little at a time, as long as the window with the most recent bytes are kept in memory. However, our implementation will assume that the full input is available and process it in one go, allowing us to focus on the compression instead of the bookkeeping required for streaming.
We will use two arrays: head maps the hash value of a four-letter prefix to a position in the input data, and prev maps a position to the previous position with the same hash value. In effect, head[h] is the head of a linked list of positions of prefixes with hash h, and prev[x] gets the element previous to x in the list.
#define LZ_WND_SIZE 32768
#define HASH_SIZE 15
#define NO_POS SIZE_MAX
#define MIN_LEN 4
/* Perform LZ77 compression on the src_len bytes in src, with back references
limited to a certain maximum distance and length, and with or without
self-overlap. Returns false as soon as either of the callback functions
returns false, otherwise returns true when all bytes have been processed. */
bool lz77_compress(const uint8_t *src, size_t src_len, size_t max_dist,
size_t max_len, bool allow_overlap,
bool (*lit_callback)(uint8_t lit, void *aux),
bool (*backref_callback)(size_t dist, size_t len, void *aux),
void *aux)
{
size_t head[1U << HASH_SIZE];
size_t prev[LZ_WND_SIZE];
uint32_t h;
size_t i, j, dist;
size_t match_len, match_pos;
size_t prev_match_len, prev_match_pos;
/* Initialize the hash table. */
for (i = 0; i < sizeof(head) / sizeof(head[0]); i++) {
head[i] = NO_POS;
}
To insert a new string position in the hash table, prev is updated to point to the previous head, and head is then updated:
static void insert_hash(uint32_t hash, size_t pos, size_t *head, size_t *prev)
{
assert(pos != NO_POS && "Invalid pos!");
prev[pos % LZ_WND_SIZE] = head[hash];
head[hash] = pos;
}
Note the modulo operation when indexing into prev: we only care about positions that fall inside the current window.
A simple function is used to compute the hash values: (read32le reads a 32-bit value in little-endian order, and is implemented in bits.h)
/* Compute a hash value based on four bytes pointed to by ptr. */
static uint32_t hash4(const uint8_t *ptr)
{
static const uint32_t HASH_MUL = 2654435761U;
/* Knuth's multiplicative hash. */
return (read32le(ptr) * HASH_MUL) >> (32 - HASH_SIZE);
}
The hash map can then be used to search efficiently for a previous match with a substring, as shown below. Searching for matches is the most computationally expensive part of the compression, so we limit how far back the list of potential matches we search.
Changing parameters such as how far back the list of prefixes to search (and whether to do lazy matching, described further down) is a way of trading less compression for more speed. The settings in our code are chosen to match those of Zlib's maximum compression level.
/* Find the longest most recent string which matches the string starting
* at src[pos]. The match must be strictly longer than prev_match_len and
* shorter or equal to max_match_len. Returns the length of the match if found
* and stores the match position in *match_pos, otherwise returns zero. */
static size_t find_match(const uint8_t *src, size_t pos, uint32_t hash,
size_t max_dist, size_t prev_match_len,
size_t max_match_len, bool allow_overlap,
const size_t *head, const size_t *prev,
size_t *match_pos)
{
size_t max_match_steps = 4096;
size_t i, l;
bool found;
size_t max_cmp;
if (prev_match_len == 0) {
/* We want backrefs of length MIN_LEN or longer. */
prev_match_len = MIN_LEN - 1;
}
if (prev_match_len >= max_match_len) {
/* A longer match would be too long. */
return 0;
}
if (prev_match_len >= 32) {
/* Do not try too hard if there is already a good match. */
max_match_steps /= 4;
}
found = false;
i = head[hash];
max_cmp = max_match_len;
/* Walk the linked list of prefix positions. */
for (i = head[hash]; i != NO_POS; i = prev[i % LZ_WND_SIZE]) {
if (max_match_steps == 0) {
break;
}
max_match_steps--;
assert(i < pos && "Matches should precede pos.");
if (pos - i > max_dist) {
/* The match is too far back. */
break;
}
if (!allow_overlap) {
max_cmp = min(max_match_len, pos - i);
if (max_cmp <= prev_match_len) {
continue;
}
}
l = cmp(src, i, pos, prev_match_len, max_cmp);
if (l != 0) {
assert(l > prev_match_len);
assert(l <= max_match_len);
found = true;
*match_pos = i;
prev_match_len = l;
if (l == max_match_len) {
/* A longer match is not possible. */
return l;
}
}
}
if (!found) {
return 0;
}
return prev_match_len;
}
/* Compare the substrings starting at src[i] and src[j], and return the length
* of the common prefix if it is strictly longer than prev_match_len
* and shorter or equal to max_match_len, otherwise return zero. */
static size_t cmp(const uint8_t *src, size_t i, size_t j,
size_t prev_match_len, size_t max_match_len)
{
size_t l;
assert(prev_match_len < max_match_len);
/* Check whether the first prev_match_len + 1 characters match. Do this
* backwards for a higher chance of finding a mismatch quickly. */
for (l = 0; l < prev_match_len + 1; l++) {
if (src[i + prev_match_len - l] !=
src[j + prev_match_len - l]) {
return 0;
}
}
assert(l == prev_match_len + 1);
/* Now check how long the full match is. */
for (; l < max_match_len; l++) {
if (src[i + l] != src[j + l]) {
break;
}
}
assert(l > prev_match_len);
assert(l <= max_match_len);
assert(memcmp(&src[i], &src[j], l) == 0);
return l;
}
With the code for finding previous matches in place, we can finish the lz77_compress function:
prev_match_len = 0;
prev_match_pos = NO_POS;
for (i = 0; i + MIN_LEN - 1 < src_len; i++) {
/* Search for a match using the hash table. */
h = hash4(&src[i]);
match_len = find_match(src, i, h, max_dist, prev_match_len,
min(max_len, src_len - i), allow_overlap,
head, prev, &match_pos);
/* Insert the current hash for future searches. */
insert_hash(h, i, head, prev);
/* If the previous match is at least as good as the current. */
if (prev_match_len != 0 && prev_match_len >= match_len) {
/* Output the previous match. */
dist = (i - 1) - prev_match_pos;
if (!backref_callback(dist, prev_match_len, aux)) {
return false;
}
/* Move past the match. */
for (j = i + 1; j < min((i - 1) + prev_match_len,
src_len - (MIN_LEN - 1)); j++) {
h = hash4(&src[j]);
insert_hash(h, j, head, prev);
}
i = (i - 1) + prev_match_len - 1;
prev_match_len = 0;
continue;
}
/* If no match (and no previous match), output literal. */
if (match_len == 0) {
assert(prev_match_len == 0);
if (!lit_callback(src[i], aux)) {
return false;
}
continue;
}
/* Otherwise the current match is better than the previous. */
if (prev_match_len != 0) {
/* Output a literal instead of the previous match. */
if (!lit_callback(src[i - 1], aux)) {
return false;
}
}
/* Defer this match and see if the next is even better. */
prev_match_len = match_len;
prev_match_pos = match_pos;
}
/* Output any previous match. */
if (prev_match_len != 0) {
dist = (i - 1) - prev_match_pos;
if (!backref_callback(dist, prev_match_len, aux)) {
return false;
}
i = (i - 1) + prev_match_len;
}
/* Output any remaining literals. */
for (; i < src_len; i++) {
if (!lit_callback(src[i], aux)) {
return false;
}
}
return true;
}
The code looks for the longest possible back reference that could be emitted at the current position. However, before outputting that back reference, it considers whether an even longer match could be found at the next position. Zlib calls this lazy match evaluation. This is still a greedy algorithm: it chooses the longest match, even though a shorter match now might allow for a longer match later and better compression overall.
Lempel–Ziv compression can be both fast and slow. Zopfli spends a lot of time trying to find optimal back references to squeeze out a few extra percent of compression. This is useful for data that is compressed once and used many times, such as static content on a web server. On the other end of the spectrum are compressors such as Snappy and LZ4, which match only against the most recent 4-byte prefix and run very fast. Such compression can be useful in database or RPC systems, where a short moment spent compressing is paid off by time savings when sending data over the network or to and from disk.
The Lempel–Ziv idea of using the source data itself as the dictionary is very elegant, but using a static dictionary can still be beneficial. Brotli is an LZ77-based compression algorithm, but it also uses a large static dictionary of strings that occur frequently on the web.
The LZ77 code is available in lz77.h and lz77.c.
Huffman Coding
The second ingredient in Zip compression is Huffman coding.
The term code in this context refers to a system for representing some data in another form. For our purposes, we are interested in codes that can be used to represent the literals and back references produced by the Lempel–Ziv compression above efficiently.
Computers traditionally represent English text using the American Standard Code for Information Interchange (ASCII). That code assigns a number to each character, and computers typically store each such number in an 8-bit byte. For example, the text you are reading now is originally stored like that. Here is the ASCII code for the upper-case English alphabet:
| A | 01000001 | N | 01001110 |
|---|---|---|---|
| B | 01000010 | O | 01001111 |
| C | 01000011 | P | 01010000 |
| D | 01000100 | Q | 01010001 |
| E | 01000101 | R | 01010010 |
| F | 01000110 | S | 01010011 |
| G | 01000111 | T | 01010100 |
| H | 01001000 | U | 01010101 |
| I | 01001001 | V | 01010110 |
| J | 01001010 | W | 01010111 |
| K | 01001011 | X | 01011000 |
| L | 01001100 | Y | 01011001 |
| M | 01001101 | Z | 01011010 |
Using one byte per character is a convenient way of storing text. It makes it easy to access or change parts of the text, and it is obvious how many bytes are required to store N characters or how many characters are stored in N bytes. However, it is not the most space efficient way. For example, E and Z are the most and least used characters in English text, respectively. Therefore it would be more space efficient to use a shorter bit representation for E and a longer for Z, instead of using the same number of bits for each character.
A code that specifies different-length codewords for different source symbols is called a variable-length code. The most famous example is Morse code, which encodes symbols using dots and dashes, originally transmitted as short and long electric pulses over a telegraph wire:
| A | • − | N | − • |
|---|---|---|---|
| B | − • • • | O | − − − |
| C | − • − • | P | • − − • |
| D | − • • | Q | − − • − |
| E | • | R | • − • |
| F | • • − • | S | • • • |
| G | − − • | T | − |
| H | • • • • | U | • • − |
| I | • • | V | • • • − |
| J | • − − − | W | • − − |
| K | − • − | X | − • • − |
| L | • − • • | Y | − • − − |
| M | − − | Z | − − • • |
One problem with Morse code is that one codeword can be the prefix of another. For example, • • − • is not uniquely decodable: it could mean either F or ER. This problem is solved by making pauses (the length of three dots) between letters during transmission. However, a better solution would be if no codeword was the prefix of another. Such a code is called a prefix-free code, or sometimes just prefix code. The fixed-length ASCII code above is trivially prefix-free since the codewords are all the same length, but variable-length codes can also be prefix-free. Telephone numbers are mostly prefix-free. Before the 112 emergency telephone number was adopted in Sweden, all existing phone numbers starting with 112 had to be changed, and nobody in the US has a phone number starting with 911.
To minimize the size of an encoded message, we would like a prefix-free code where frequently occurring symbols have shorter codewords than infrequent ones. The optimum code would be one which generates the shortest possible result, that is, a code where the sum of the codeword lengths multiplied by their frequency of occurrence is as small as possible. This is called a minimum-redundancy prefix-free code, or these days a Huffman code after the man who invented an efficient algorithm for constructing them.
Huffman's Algorithm
While studying for his doctorate in electrical engineering at MIT, David A. Huffman took a course in information theory taught by Robert Fano. According to legend, Fano gave his students a choice between taking a final exam or writing a term paper. Huffman chose the latter, and was assigned the topic of finding minimum-redundancy prefix-free codes. Huffman was allegedly not aware that this was an open problem which Fano himself had worked on (the best known method at the time was Shannon-Fano coding). Huffman's paper was published as A Method for the Construction of Minimum-Redundancy Codes in 1952, and the algorithm has been widely used ever since.

David A. Huffman (1925–1999). Photo from UC Santa Cruz press release.
Huffman's algorithm creates a minimum-redundancy prefix-free code for a set of symbols and their frequencies of use. The algorithm works by repeatedly selecting the two symbols, say X and Y, with the lowest frequencies from the set, and replacing them with a single composite symbol which represents "X or Y". The frequency of the composite symbol is the sum of the frequencies of the two original symbols. The codewords for X and Y can be whatever codeword gets assigned to the composite "X or Y" symbol, followed by a 0 or 1 to differentiate between the two original symbols. When the set has been reduced to a single symbol, the algorithm is done. (See this video for a good explanation.)
Below is an example of running the algorithm on a small set of symbols:
| Symbol | Frequency |
|---|---|
| A | 6 |
| B | 4 |
| C | 2 |
| D | 3 |
Initially, the set of symbols to be processed (coloured blue) is our original symbols:
The two lowest-frequency symbols, C and D, are removed from the set, and replaced by a composite symbol whose frequency is the sum of C and D's frequencies.
The lowest-frequency symbols are now B and the composite symbol with frequency five. These are removed from the set, and a new composite symbol with frequency nine is inserted instead:
Finally, A and the composite node with frequency 9 have the lowest frequencies, and so a composite node with frequency 15 is inserted.
Since there is only one node left in the set, the algorithm is finished.
The algorithm leaves us with a structure called a Huffman tree. Note how it has our input symbols as leaves, and symbols with higher frequency are closer to the top. We can derive codewords for our symbols from this tree by starting at the root, walking towards a symbol, and adding a 0 or 1 to the codeword when going left or right, respectively. If we do that, we end up with:
| Symbol | codeword |
|---|---|
| A | 0 |
| B | 10 |
| C | 110 |
| D | 111 |
Note how none of the codewords are a prefix of another, and how the symbols with higher frequency have shorter codewords.
The tree can also be used for decoding: start at the root and go left or right for 0 or 1 until a symbol is reached. For example, the string 010100 decodes to ABBA.
Note that the length of each codeword equals the depth of the corresponding node in the tree. As we will see in the next section, we do not need the actual tree to assign codewords; knowing the lengths of the codewords is enough. Therefore, the output of our implementation of Huffman's algorithm will be those codeword lengths.
To store the set of symbols and efficiently find the one with lowest frequency, we use a binary heap data structure, specifically a min-heap since we want the minimum value on top.
/* Swap the 32-bit values pointed to by a and b. */
static void swap32(uint32_t *a, uint32_t *b)
{
uint32_t tmp;
tmp = *a;
*a = *b;
*b = tmp;
}
/* Move element i in the n-element heap down to restore the minheap property. */
static void minheap_down(uint32_t *heap, size_t n, size_t i)
{
size_t left, right, min;
assert(i >= 1 && i <= n && "i must be inside the heap");
/* While the i-th element has at least one child. */
while (i * 2 <= n) {
left = i * 2;
right = i * 2 + 1;
/* Find the child with lowest value. */
min = left;
if (right <= n && heap[right] < heap[left]) {
min = right;
}
/* Move i down if it is larger. */
if (heap[min] < heap[i]) {
swap32(&heap[min], &heap[i]);
i = min;
} else {
break;
}
}
}
/* Establish minheap property for heap[1..n]. */
static void minheap_heapify(uint32_t *heap, size_t n)
{
size_t i;
/* Floyd's algorithm. */
for (i = n / 2; i >= 1; i--) {
minheap_down(heap, n, i);
}
}
To keep track of the frequency of up to n symbols we will use a heap of n elements. In addition, every time we create a composite symbol, we want to "link" the two original symbols to the new one. So each symbol will also have a "link element".
We will use a single array of n * 2 + 1 elements to store the n-element heap and the n link elements. When two symbols in the heap are replaced by one, we will use the leftover array element to store the link of the new symbol. This is based on the implementation in Witten, Moffat and Bell's Managing Gigabytes.
In each heap node, we will use the upper 16 bits to store the symbol's frequency, and the lower 16 bits to store the index of the symbol's link element. By using the upper bits, the difference in frequency will determine the outcome of 32-bit comparisons between two heap elements.
Because of this representation, we must be sure that a symbol's frequency always fits within 16 bits. When the algorithm is finished, the final composite symbol will have the frequency of all original symbols combined, so therefore this sum must fit within 16 bits. Our Deflate implementation will make sure of this by processing at most 65,535 symbols at a time.
Symbols with zero frequency will receive a codeword length of zero and not take part in the construction of the code.
If a codeword exceeds the maximum length, we "flatten" the distribution of symbol frequencies by right-shifting them and try again (yes, with a goto). There are more sophisticated ways of doing length-limited Huffman coding, but this is simple and effective.
#define MAX_HUFFMAN_SYMBOLS 288 /* Deflate uses max 288 symbols. */
/* Construct a Huffman code for n symbols with the frequencies in freq, and
* codeword length limited to max_len. The sum of the frequencies must be <=
* UINT16_MAX. max_len must be large enough that a code is always possible,
* i.e. 2 ** max_len >= n. Symbols with zero frequency are not part of the code
* and get length zero. Outputs the codeword lengths in lengths[0..n-1]. */
static void compute_huffman_lengths(const uint16_t *freqs, size_t n,
uint8_t max_len, uint8_t *lengths)
{
uint32_t nodes[MAX_HUFFMAN_SYMBOLS * 2 + 1], p, q;
uint16_t freq;
size_t i, h, l;
uint16_t freq_shift = 0;
#ifndef NDEBUG
uint32_t freq_sum = 0;
for (i = 0; i < n; i++) {
freq_sum += freqs[i];
}
assert(freq_sum <= UINT16_MAX && "Frequency sum too large!");
#endif
assert(n <= MAX_HUFFMAN_SYMBOLS);
assert((1U << max_len) >= n && "max_len must be large enough");
try_again:
/* Initialize the heap. h is the heap size. */
h = 0;
for (i = 0; i < n; i++) {
freq = freqs[i];
if (freq == 0) {
continue; /* Ignore zero-frequency symbols. */
}
/* Shift frequencies down towards 1. */
freq >>= freq_shift;
if (freq == 0) {
freq = 1;
}
/* High 16 bits: Symbol frequency.
Low 16 bits: Symbol link element index. */
h++;
nodes[h] = ((uint32_t)freq << 16) | (uint32_t)(n + h);
}
minheap_heapify(nodes, h);
/* Special case for fewer than two non-zero symbols. */
if (h < 2) {
for (i = 0; i < n; i++) {
lengths[i] = (freqs[i] == 0) ? 0 : 1;
}
return;
}
/* Build the Huffman tree. */
while (h > 1) {
/* Remove the lowest frequency node p from the heap. */
p = nodes[1];
nodes[1] = nodes[h--];
minheap_down(nodes, h, 1);
/* Get q, the next lowest frequency node. */
q = nodes[1];
/* Replace q with a new symbol with the combined frequencies of
p and q, and with the no longer used h+1'th node as the
link element. */
nodes[1] = ((p & 0xffff0000) + (q & 0xffff0000))
| (uint32_t)(h + 1);
/* Set the links of p and q to point to the link element of
the new node. */
nodes[p & 0xffff] = nodes[q & 0xffff] = (uint32_t)(h + 1);
/* Move the new symbol down to restore heap property. */
minheap_down(nodes, h, 1);
}
/* Compute the codeword length for each symbol. */
h = 0;
for (i = 0; i < n; i++) {
if (freqs[i] == 0) {
lengths[i] = 0;
continue;
}
h++;
/* Link element for the i-th symbol. */
p = nodes[n + h];
/* Follow the links until we hit the root (link index 2). */
l = 1;
while (p != 2) {
l++;
p = nodes[p];
}
if (l > max_len) {
/* Push freqs lower. */
assert(freq_shift != 15 && "freq_shift too high!");
freq_shift++;
goto try_again;
}
assert(l <= UINT8_MAX);
lengths[i] = (uint8_t)l;
}
}
An elegant alternative to the binary heap approach is to store the symbols in two queues. The first queue contains the original symbols, sorted by frequency. When a composite symbol is created, it is added to the second queue. This way, the lowest-frequency symbol will always be found at the front of one of the queues. This was described by Jan van Leeuwen in On the Construction of Huffman Trees (1976).
While Huffman codes are optimal as far as prefix-free codes go, there are more efficient ways to encode data beyond prefix coding, such as Arithmetic coding and Asymmetric numeral systems.
Canonical Huffman Codes
In the earlier example we ended up with the Huffman tree below.
By walking down the tree from the root and using 0 for left branches and 1 for right branches, we ended up with the following code:
| Symbol | codeword |
|---|---|
| A | 0 |
| B | 10 |
| C | 110 |
| D | 111 |
The decision to use 0 for left 1 for right branches seems arbitrary. If we do the reverse we get:
| Symbol | codeword |
|---|---|
| A | 1 |
| B | 01 |
| C | 001 |
| D | 000 |
In fact, we can label the two edges from a node with 0 or 1 arbitrarily (as long as the labels are different) and still end up with an equivalent code:
| Symbol | codeword |
|---|---|
| A | 0 |
| B | 11 |
| C | 100 |
| D | 101 |
This shows that while Huffman's algorithm gives the requisite codeword lengths for a minimum-redundancy prefix-free code, there are many ways of assigning the individual codewords.
Given codeword lengths computed by Huffman's algorithm, a Canonical Huffman code assigns codewords to symbols in a specific way. This is useful because it makes it sufficient to store and transmit the codeword lengths with the compressed data: the decoder can reconstruct the codewords based on the lengths. (One could of course also store and transmit the symbol frequencies and run Huffman's algorithm in the decoder, but that would require more work for the decoder and likely more storage space too.) Another very important property is that the structure of canonical codes facilitates efficient decoding.
The idea is to assign codewords to the symbols sequentially, one codeword length at a time. The initial codeword is 0. The next codeword of some length is the previous one plus 1. The first codeword of length N is constructed by taking the last codeword of length N-1, adding one (to get a new codeword) and shifting left one step (to increase the length).
Viewed in terms of a Huffman tree, codewords are assigned in sequence to the leaves in left-to-right order, one level at a time, shifting left when we move down one level.
In our A, B, C, D example, Huffman's algorithm gave codeword lengths 1,2,3,3. The first codeword is 0. That is also the last codeword of length 1. For length 2, we take the 0, add 1 to get the next code which will be the prefix of the two-bit codes: we shift it left and obtain 10. That is also the last codeword of length 2. To get to length 3, we add one and shift: 110. To get the next one of length 3, we add one: 111.
| Symbol | codeword |
|---|---|
| A | 0 |
| B | 10 |
| C | 110 |
| D | 111 |
The implementation for generating the canonical codes is shown below. Note that the Deflate algorithm expects codewords to be emitted LSB-first, that is, the first bit of a codeword should be stored in the least significant bit. This means we have to reverse the bits, which can be done using a lookup table.
#define MAX_HUFFMAN_BITS 16 /* Implode uses max 16-bit codewords. */
static void compute_canonical_code(uint16_t *codewords, const uint8_t *lengths,
size_t n)
{
size_t i;
uint16_t count[MAX_HUFFMAN_BITS + 1] = {0};
uint16_t code[MAX_HUFFMAN_BITS + 1];
int l;
/* Count the number of codewords of each length. */
for (i = 0; i < n; i++) {
count[lengths[i]]++;
}
count[0] = 0; /* Ignore zero-length codes. */
/* Compute the first codeword for each length. */
code[0] = 0;
for (l = 1; l <= MAX_HUFFMAN_BITS; l++) {
code[l] = (uint16_t)((code[l - 1] + count[l - 1]) << 1);
}
/* Assign a codeword for each symbol. */
for (i = 0; i < n; i++) {
l = lengths[i];
if (l == 0) {
continue;
}
codewords[i] = reverse16(code[l]++, l); /* Make it LSB-first. */
}
}
/* Reverse the n least significant bits of x.
The (16 - n) most significant bits of the result will be zero. */
static inline uint16_t reverse16(uint16_t x, int n)
{
uint16_t lo, hi;
uint16_t reversed;
assert(n > 0);
assert(n <= 16);
lo = x & 0xff;
hi = x >> 8;
reversed = (uint16_t)((reverse8_tbl[lo] << 8) | reverse8_tbl[hi]);
return reversed >> (16 - n);
}
With all the parts now in place, we can write the code to initialize the encoder:
typedef struct huffman_encoder_t huffman_encoder_t;
struct huffman_encoder_t {
uint16_t codewords[MAX_HUFFMAN_SYMBOLS]; /* LSB-first codewords. */
uint8_t lengths[MAX_HUFFMAN_SYMBOLS]; /* Codeword lengths. */
};
/* Initialize a Huffman encoder based on the n symbol frequencies. */
void huffman_encoder_init(huffman_encoder_t *e, const uint16_t *freqs, size_t n,
uint8_t max_codeword_len)
{
assert(n <= MAX_HUFFMAN_SYMBOLS);
assert(max_codeword_len <= MAX_HUFFMAN_BITS);
compute_huffman_lengths(freqs, n, max_codeword_len, e->lengths);
compute_canonical_code(e->codewords, e->lengths, n);
}
We also provide a function for setting up an encoder based on already computed code lengths:
/* Initialize a Huffman encoder based on the n codeword lengths. */
void huffman_encoder_init2(huffman_encoder_t *e, const uint8_t *lengths,
size_t n)
{
size_t i;
for (i = 0; i < n; i++) {
e->lengths[i] = lengths[i];
}
compute_canonical_code(e->codewords, e->lengths, n);
}
Efficient Huffman Decoding
The most basic way of doing Huffman decoding is to walk the Huffman tree from the root, reading one bit of input at a time to decide whether to take the next left or right branch. Once a leaf node is reached, that is the decoded symbol.
The method above is often taught at universities and in textbooks. It is simple and elegant, but processing one bit at a time is relatively slow. A very fast way of decoding is to use a lookup table. For the code above where the max codeword length is three bits, we could use the following table:
| Bits | Symbol | Codeword Length |
|---|---|---|
| 000 | A | 1 |
| 001 | A | 1 |
| 010 | A | 1 |
| 011 | A | 1 |
| 100 | B | 2 |
| 101 | B | 2 |
| 110 | C | 3 |
| 111 | D | 3 |
Although there are only four symbols, the table needs to have eight entries to cover all possible three-bit inputs. Symbols with codewords shorter than three bits have multiple entries in the table. For example, the 10 codeword has been "padded" to 100 and 101 to cover all three-bit inputs starting with 10.
To perform decoding using this method, one would index into the table using the next three bits of input, and immediately find the corresponding symbol and its codeword length. The length is important, because even though we looked at the next three bits, we should only consume as many bits of input as the actual codeword is long.
The lookup table approach is very fast, but there is a downside: the table size doubles with each extra bit of codeword length. This means that building the table becomes exponentially slower, and using it may also become slower if it no longer fits in the CPU's cache.
Because of this, a lookup table is typically only used for codewords up to a certain length, and some other approach is used for longer codewords. As Huffman coding assigns shorter codewords to more frequent symbols, using a lookup table for short codewords is a great optimization for the common case.
The method used by Zlib is to have multiple levels of lookup tables. If a codeword is too long for the first table, the table entry will point to a secondary table, to be indexed with the remaining bits.
However, there is another very elegant method based on the properties of canonical Huffman codes. This is described in On the Implementation of Minimum Redundancy Prefix Codes (Moffat and Turpin 1997) and further explained in Charles Bloom's The Lost Huffman Paper.
Consider the codewords from our canonical code above: 0, 10, 110, 111. We will keep track of the first codeword of each length, and where in the sequence of assigned codewords it is, the "symbol index".
| Codeword Length | First Codeword | First Symbol Index |
|---|---|---|
| 1 | 0 | 1 (A) |
| 2 | 10 | 2 (B) |
| 3 | 110 | 3 (C) |
Because the codewords are assigned sequentially, once we know how many bits of input to consider, the table above lets us find out what symbol index those bits represent. For example, for the 3-bit input 111, we see that this is at offset 1 from the first codeword of that length (110). The first symbol index of that length is 3, and the offset of 1 takes us to symbol index 4. Another table maps the symbol index to the symbol:
sym_idx = d->first_symbol[len] + (bits - d->first_code[len]);
sym = d->syms[sym_idx];
As a small optimization, instead of storing the first symbol index and first codeword separately, we can store the first symbol index minus the first codeword in a table:
sym_idx = d->offset_first_sym_idx[len] + bits;
sym = d->syms[sym_idx];
To determine how many bits of input to consider, we again use the sequential property of the code. In our example code, the valid 1-bit codewords are all strictly less than 1, the 2-bit codewords are strictly less than 11, and the 3-bit codewords are strictly less than 1000 (trivially true for all 3-bit values). In other words, a valid N-bit codeword must be strictly less than the first N-bit codeword plus the number of N-bit codewords. What is even more exciting is that we can left-shift those limits so that they are all 3 bits wide. Let us call them the sentinel bits for each codeword length:
| Codeword Length | Sentinel Bits |
|---|---|
| 1 | 100 |
| 2 | 110 |
| 3 | 1000 |
(The length 3 sentinel has overflowed to 4 bits, but that just means any 3-bit input will do.)
This means we can look at three bits of input and compare against the sentinel bits to figure out how long our codeword is. Once that is done, we shift the input bits as to only consider the right number of them, and then find the symbol index as shown above:
for (len = 1; len <= 3; len++) {
if (bits < d->sentinel_bits[len]) {
bits >>= 3 - len; /* Get the len most significant bits. */
sym_idx = d->offset_first_sym_idx[len] + bits;
}
}
The time complexity of this is linear in the number of codeword bits, but it is space efficient, requires only a load and comparison per step, and since shorter codewords are more frequent it optimizes for the common case.
The full decoder is shown below:
#define HUFFMAN_LOOKUP_TABLE_BITS 8 /* Seems a good trade-off. */
typedef struct huffman_decoder_t huffman_decoder_t;
struct huffman_decoder_t {
/* Lookup table for fast decoding of short codewords. */
struct {
uint16_t sym : 9; /* Wide enough to fit the max symbol nbr. */
uint16_t len : 7; /* 0 means no symbol. */
} table[1U << HUFFMAN_LOOKUP_TABLE_BITS];
/* "Sentinel bits" value for each codeword length. */
uint32_t sentinel_bits[MAX_HUFFMAN_BITS + 1];
/* First symbol index minus first codeword mod 2**16 for each length. */
uint16_t offset_first_sym_idx[MAX_HUFFMAN_BITS + 1];
/* Map from symbol index to symbol. */
uint16_t syms[MAX_HUFFMAN_SYMBOLS];
#ifndef NDEBUG
size_t num_syms;
#endif
};
/* Get the n least significant bits of x. */
static inline uint64_t lsb(uint64_t x, size_t n)
{
assert(n <= 63);
return x & (((uint64_t)1 << n) - 1);
}
/* Use the decoder d to decode a symbol from the LSB-first zero-padded bits.
* Returns the decoded symbol number or -1 if no symbol could be decoded.
* *num_used_bits will be set to the number of bits used to decode the symbol,
* or zero if no symbol could be decoded. */
static inline int huffman_decode(const huffman_decoder_t *d, uint16_t bits,
size_t *num_used_bits)
{
uint64_t lookup_bits;
size_t l;
size_t sym_idx;
/* First try the lookup table. */
lookup_bits = lsb(bits, HUFFMAN_LOOKUP_TABLE_BITS);
assert(lookup_bits < sizeof(d->table) / sizeof(d->table[0]));
if (d->table[lookup_bits].len != 0) {
assert(d->table[lookup_bits].len <= HUFFMAN_LOOKUP_TABLE_BITS);
assert(d->table[lookup_bits].sym < d->num_syms);
*num_used_bits = d->table[lookup_bits].len;
return d->table[lookup_bits].sym;
}
/* Then do canonical decoding with the bits in MSB-first order. */
bits = reverse16(bits, MAX_HUFFMAN_BITS);
for (l = HUFFMAN_LOOKUP_TABLE_BITS + 1; l <= MAX_HUFFMAN_BITS; l++) {
if (bits < d->sentinel_bits[l]) {
bits >>= MAX_HUFFMAN_BITS - l;
sym_idx = (uint16_t)(d->offset_first_sym_idx[l] + bits);
assert(sym_idx < d->num_syms);
*num_used_bits = l;
return d->syms[sym_idx];
}
}
*num_used_bits = 0;
return -1;
}
To set up the decoder, we compute the canonical code similarly to huffman_encoder_init and fill in the various tables:
/* Initialize huffman decoder d for a code defined by the n codeword lengths.
Returns false if the codeword lengths do not correspond to a valid prefix
code. */
bool huffman_decoder_init(huffman_decoder_t *d, const uint8_t *lengths,
size_t n)
{
size_t i;
uint16_t count[MAX_HUFFMAN_BITS + 1] = {0};
uint16_t code[MAX_HUFFMAN_BITS + 1];
uint32_t s;
uint16_t sym_idx[MAX_HUFFMAN_BITS + 1];
int l;
#ifndef NDEBUG
assert(n <= MAX_HUFFMAN_SYMBOLS);
d->num_syms = n;
#endif
/* Zero-initialize the lookup table. */
for (i = 0; i < sizeof(d->table) / sizeof(d->table[0]); i++) {
d->table[i].len = 0;
}
/* Count the number of codewords of each length. */
for (i = 0; i < n; i++) {
assert(lengths[i] <= MAX_HUFFMAN_BITS);
count[lengths[i]]++;
}
count[0] = 0; /* Ignore zero-length codewords. */
/* Compute sentinel_bits and offset_first_sym_idx for each length. */
code[0] = 0;
sym_idx[0] = 0;
for (l = 1; l <= MAX_HUFFMAN_BITS; l++) {
/* First canonical codeword of this length. */
code[l] = (uint16_t)((code[l - 1] + count[l - 1]) << 1);
if (count[l] != 0 && code[l] + count[l] - 1 > (1 << l) - 1) {
/* The last codeword is longer than l bits. */
return false;
}
s = (uint32_t)((code[l] + count[l]) << (MAX_HUFFMAN_BITS - l));
d->sentinel_bits[l] = s;
assert(d->sentinel_bits[l] >= code[l] && "No overflow!");
sym_idx[l] = sym_idx[l - 1] + count[l - 1];
d->offset_first_sym_idx[l] = sym_idx[l] - code[l];
}
/* Build mapping from index to symbol and populate the lookup table. */
for (i = 0; i < n; i++) {
l = lengths[i];
if (l == 0) {
continue;
}
d->syms[sym_idx[l]] = (uint16_t)i;
sym_idx[l]++;
if (l <= HUFFMAN_LOOKUP_TABLE_BITS) {
table_insert(d, i, l, code[l]);
code[l]++;
}
}
return true;
}
static void table_insert(huffman_decoder_t *d, size_t sym, int len,
uint16_t codeword)
{
int pad_len;
uint16_t padding, index;
assert(len <= HUFFMAN_LOOKUP_TABLE_BITS);
codeword = reverse16(codeword, len); /* Make it LSB-first. */
pad_len = HUFFMAN_LOOKUP_TABLE_BITS - len;
/* Pad the pad_len upper bits with all bit combinations. */
for (padding = 0; padding < (1U << pad_len); padding++) {
index = (uint16_t)(codeword | (padding << len));
d->table[index].sym = (uint16_t)sym;
d->table[index].len = (uint16_t)len;
assert(d->table[index].sym == sym && "Fits in bitfield.");
assert(d->table[index].len == len && "Fits in bitfield.");
}
}
Deflate
Deflate, introduced with PKZip 2.04c in 1993, is the default compression method in modern Zip files. It is also the compression method used in gzip, PNG, and many other file formats. It uses LZ77 compression and Huffman coding in a combination which will be described and implemented in this section.
Before Deflate, PKZip used compression methods called Shrink, Reduce, and Implode. Although those methods are rarely seen in use today, they were still in use some time after the introduction of Deflate since they required less memory. Those legacy methods are covered in a follow-up article.
Bitstreams
Deflate stores Huffman codewords in a least-significant-bit-first (LSB-first) bitstream, meaning that the first bit of the stream is stored in the least significant bit of the first byte.
For example, consider this bit stream (read left-to-right): 1-0-0-1-1. When stored LSB-first in a byte, the byte's value becomes 0b00011001 (binary) or 0x19 (hexadecimal). This might seem backwards (in a sense it is), but one advantage is that it makes it easy to get the first N bits from a computer word: just mask off the N lowest bits.
The following routines are from bitstream.h.
/* Input bitstream. */
typedef struct istream_t istream_t;
struct istream_t {
const uint8_t *src; /* Source bytes. */
const uint8_t *end; /* Past-the-end byte of src. */
size_t bitpos; /* Position of the next bit to read. */
size_t bitpos_end; /* Position of past-the-end bit. */
};
/* Initialize an input stream to present the n bytes from src as an LSB-first
* bitstream. */
static inline void istream_init(istream_t *is, const uint8_t *src, size_t n)
{
is->src = src;
is->end = src + n;
is->bitpos = 0;
is->bitpos_end = n * 8;
}
For our Huffman decoder, we want to look at the next bits in the stream (enough bits for the longest possible codeword), and then advance the stream by the number of bits used by the decoded symbol:
#define ISTREAM_MIN_BITS (64 - 7)
/* Get the next bits from the input stream. The number of bits returned is
* between ISTREAM_MIN_BITS and 64, depending on the position in the stream, or
* fewer if the end of stream is reached. The upper bits are zero-padded. */
static inline uint64_t istream_bits(const istream_t *is)
{
const uint8_t *next;
uint64_t bits;
int i;
next = &is->src[is->bitpos / 8];
assert(next <= is->end && "Cannot read past end of stream.");
if (is->end - next >= 8) {
/* Common case: read 8 bytes in one go. */
bits = read64le(next);
} else {
/* Read the available bytes and zero-pad. */
bits = 0;
for (i = 0; i < is->end - next; i++) {
bits |= (uint64_t)next[i] << (i * 8);
}
}
return bits >> (is->bitpos % 8);
}
/* Advance n bits in the bitstream if possible. Returns false if that many bits
* are not available in the stream. */
static inline bool istream_advance(istream_t *is, size_t n) {
assert(is->bitpos <= is->bitpos_end);
if (is->bitpos_end - is->bitpos < n) {
return false;
}
is->bitpos += n;
return true;
}
The intention is that in the common case, istream_bits can execute as a single load instruction and some arithmetic on 64-bit machines, assuming the members of the istream_t struct are available in registers. read64le is implemented in bits.h (modern compilers translate it to a single 64-bit load on little-endian):
/* Read a 64-bit value from p in little-endian byte order. */
static inline uint64_t read64le(const uint8_t *p)
{
/* The one true way, see
* https://commandcenter.blogspot.com/2012/04/byte-order-fallacy.html */
return ((uint64_t)p[0] << 0) |
((uint64_t)p[1] << 8) |
((uint64_t)p[2] << 16) |
((uint64_t)p[3] << 24) |
((uint64_t)p[4] << 32) |
((uint64_t)p[5] << 40) |
((uint64_t)p[6] << 48) |
((uint64_t)p[7] << 56);
}
We also need a function to advance the bitstream to the next byte boundary:
/* Round x up to the next multiple of m, which must be a power of 2. */
static inline size_t round_up(size_t x, size_t m)
{
assert((m & (m - 1)) == 0 && "m must be a power of two");
return (x + m - 1) & (size_t)(-m); /* Hacker's Delight (2nd), 3-1. */
}
/* Align the input stream to the next 8-bit boundary and return a pointer to
* that byte, which may be the past-the-end-of-stream byte. */
static inline const uint8_t *istream_byte_align(istream_t *is)
{
const uint8_t *byte;
assert(is->bitpos <= is->bitpos_end && "Not past end of stream.");
is->bitpos = round_up(is->bitpos, 8);
byte = &is->src[is->bitpos / 8];
assert(byte <= is->end);
return byte;
}
For the output bitstream, we write bits using a read-modify-write sequence. In the fast case, a bit write can be done by a 64-bit read, some bit operations, and a 64-bit write.
/* Output bitstream. */
typedef struct ostream_t ostream_t;
struct ostream_t {
uint8_t *dst;
uint8_t *end;
size_t bitpos;
size_t bitpos_end;
};
/* Initialize an output stream to write LSB-first bits into dst[0..n-1]. */
static inline void ostream_init(ostream_t *os, uint8_t *dst, size_t n)
{
os->dst = dst;
os->end = dst + n;
os->bitpos = 0;
os->bitpos_end = n * 8;
}
/* Get the current bit position in the stream. */
static inline size_t ostream_bit_pos(const ostream_t *os)
{
return os->bitpos;
}
/* Return the number of bytes written to the output buffer. */
static inline size_t ostream_bytes_written(ostream_t *os)
{
return round_up(os->bitpos, 8) / 8;
}
/* Write n bits to the output stream. Returns false if there is not enough room
* at the destination. */
static inline bool ostream_write(ostream_t *os, uint64_t bits, size_t n)
{
uint8_t *p;
uint64_t x;
size_t shift, i;
assert(n <= 57);
assert(bits <= ((uint64_t)1 << n) - 1 && "Must fit in n bits.");
if (os->bitpos_end - os->bitpos < n) {
/* Not enough room. */
return false;
}
p = &os->dst[os->bitpos / 8];
shift = os->bitpos % 8;
if (os->end - p >= 8) {
/* Common case: read and write 8 bytes in one go. */
x = read64le(p);
x = lsb(x, shift);
x |= bits << shift;
write64le(p, x);
} else {
/* Slow case: read/write as many bytes as are available. */
x = 0;
for (i = 0; i < (size_t)(os->end - p); i++) {
x |= (uint64_t)p[i] << (i * 8);
}
x = lsb(x, shift);
x |= bits << shift;
for (i = 0; i < (size_t)(os->end - p); i++) {
p[i] = (uint8_t)(x >> (i * 8));
}
}
os->bitpos += n;
return true;
}
/* Write a 64-bit value x to dst in little-endian byte order. */
static inline void write64le(uint8_t *dst, uint64_t x)
{
dst[0] = (uint8_t)(x >> 0);
dst[1] = (uint8_t)(x >> 8);
dst[2] = (uint8_t)(x >> 16);
dst[3] = (uint8_t)(x >> 24);
dst[4] = (uint8_t)(x >> 32);
dst[5] = (uint8_t)(x >> 40);
dst[6] = (uint8_t)(x >> 48);
dst[7] = (uint8_t)(x >> 56);
}
We also want an efficient way of writing bytes to the stream. One could of course perform repeated 8-bit writes, but using memcpy is much faster:
/* Align the bitstream to the next byte boundary, then write the n bytes from
src to it. Returns false if there is not enough room in the stream. */
static inline bool ostream_write_bytes_aligned(ostream_t *os,
const uint8_t *src,
size_t n)
{
if (os->bitpos_end - round_up(os->bitpos, 8) < n * 8) {
return false;
}
os->bitpos = round_up(os->bitpos, 8);
memcpy(&os->dst[os->bitpos / 8], src, n);
os->bitpos += n * 8;
return true;
}
Decompression (Inflation)
Since the compression algorithm is called Deflate—to let the air out of something—the decompression process is sometimes referred to as Inflation. Studying this process first will give us an understanding of how the format works. The code is available in the first part of deflate.h and deflate.c, bits.h, tables.h, and tables.c (generated by generate_tables.c).
Deflate-compressed data is stored as a series of blocks. Each block starts with a 3-bit header where the first (least significant) bit is set if this is the final block of the series, and the other two bits indicate the block type.
There are three block types: uncompressed (0), compressed with fixed Huffman codes (1) and compressed with "dynamic" Huffman codes (2).
The following code drives the decompression, relying on helper functions for the different block types which will be implemented further below.
typedef enum {
HWINF_OK, /* Inflation was successful. */
HWINF_FULL, /* Not enough room in the output buffer. */
HWINF_ERR /* Error in the input data. */
} inf_stat_t;
/* Decompress (inflate) the Deflate stream in src. The number of input bytes
used, at most src_len, is stored in *src_used on success. Output is written
to dst. The number of bytes written, at most dst_cap, is stored in *dst_used
on success. src[0..src_len-1] and dst[0..dst_cap-1] must not overlap. */
inf_stat_t hwinflate(const uint8_t *src, size_t src_len, size_t *src_used,
uint8_t *dst, size_t dst_cap, size_t *dst_used)
{
istream_t is;
size_t dst_pos;
uint64_t bits;
bool bfinal;
inf_stat_t s;
istream_init(&is, src, src_len);
dst_pos = 0;
do {
/* Read the 3-bit block header. */
bits = istream_bits(&is);
if (!istream_advance(&is, 3)) {
return HWINF_ERR;
}
bfinal = bits & 1;
bits >>= 1;
switch (lsb(bits, 2)) {
case 0: /* 00: No compression. */
s = inf_noncomp_block(&is, dst, dst_cap, &dst_pos);
break;
case 1: /* 01: Compressed with fixed Huffman codes. */
s = inf_fixed_block(&is, dst, dst_cap, &dst_pos);
break;
case 2: /* 10: Compressed with "dynamic" Huffman codes. */
s = inf_dyn_block(&is, dst, dst_cap, &dst_pos);
break;
default: /* Invalid block type. */
return HWINF_ERR;
}
if (s != HWINF_OK) {
return s;
}
} while (!bfinal);
*src_used = (size_t)(istream_byte_align(&is) - src);
assert(dst_pos <= dst_cap);
*dst_used = dst_pos;
return HWINF_OK;
}
Non-Compressed Deflate Blocks
The simplest block type is the non-compressed or "stored" block. It begins at the next 8-bit boundary of the bitstream, with a 16-bit word (len) indicating the length of the block, followed by another 16-bit word (nlen) which is the ones' complement (all bits inverted) of len. The idea is presumably that nlen acts as a simple checksum of len: if the file is corrupted, it is likely that the values are no longer each others' complements, and the program can detect the error.
After len and nlen follows the non-compressed data. Because the block length is a 16-bit value, it is limited to 65,535 bytes.
static inf_stat_t inf_noncomp_block(istream_t *is, uint8_t *dst,
size_t dst_cap, size_t *dst_pos)
{
const uint8_t *p;
uint16_t len, nlen;
p = istream_byte_align(is);
/* Read len and nlen (2 x 16 bits). */
if (!istream_advance(is, 32)) {
return HWINF_ERR; /* Not enough input. */
}
len = read16le(p);
nlen = read16le(p + 2);
p += 4;
if (nlen != (uint16_t)~len) {
return HWINF_ERR;
}
if (!istream_advance(is, len * 8)) {
return HWINF_ERR; /* Not enough input. */
}
if (dst_cap - *dst_pos < len) {
return HWINF_FULL; /* Not enough room to output. */
}
memcpy(&dst[*dst_pos], p, len);
*dst_pos += len;
return HWINF_OK;
}
Fixed Huffman Code Deflate Blocks
Compressed Deflate blocks use Huffman codes to represent a sequence of LZ77 literals and back references terminated by an end-of-block marker. One Huffman code, the litlen code, is used for literals, back reference lengths, and the end-of-block marker. A second code, the dist code, is used for back reference distances.
The litlen code encodes values between 0 and 285. Values 0 through 255 represent literal bytes, 256 is the end-of-block marker, and values 257 through 285 represent back reference lengths.
Back references are between 3 and 258 bytes long. The litlen value determines a base length to which zero or more extra bits from the stream are added to get the full length according to the table below. For example, a litlen value of 269 indicates a base length of 19 and two extra bits. Adding the next two bits from the stream yields a final length between 19 and 22.
| Litlen | Extra Bits | Length(s) |
|---|---|---|
| 257 | 0 | 3 |
| 258 | 0 | 4 |
| 259 | 0 | 5 |
| 260 | 0 | 6 |
| 261 | 0 | 7 |
| 262 | 0 | 8 |
| 263 | 0 | 9 |
| 264 | 0 | 10 |
| 265 | 1 | 11–12 |
| 266 | 1 | 13–14 |
| 267 | 1 | 15–16 |
| 268 | 1 | 17–18 |
| 269 | 2 | 19–22 |
| 270 | 2 | 23–26 |
| 271 | 2 | 27–30 |
| 272 | 2 | 31–34 |
| 273 | 3 | 35–42 |
| 274 | 3 | 43–50 |
| 275 | 3 | 51–58 |
| 276 | 3 | 59–66 |
| 277 | 4 | 67–82 |
| 278 | 4 | 83–98 |
| 279 | 4 | 99–114 |
| 280 | 4 | 115–130 |
| 281 | 5 | 131–162 |
| 282 | 5 | 163–194 |
| 283 | 5 | 195–226 |
| 284 | 5 | 227–257 |
| 285 | 0 | 258 |
(Note that litlen value 284 plus five extra bits could actually represents lengths 227–258, but the specification indicates that 258, the maximum back reference length, should be represented using a separate litlen value. This is presumably to allow for a shorter encoding in cases where the maximum length is common.)
The decompressor uses a table that maps from litlen value (minus 257) to base length and extra bits:
/* Table of litlen symbol values minus 257 with corresponding base length
and number of extra bits. */
struct litlen_tbl_t {
uint16_t base_len : 9;
uint16_t ebits : 7;
};
const struct litlen_tbl_t litlen_tbl[29] = {
/* 257 */ { 3, 0 },
/* 258 */ { 4, 0 },
...
/* 284 */ { 227, 5 },
/* 285 */ { 258, 0 }
};
The fixed litlen Huffman code is a canonical code using the following codeword lengths (286–287 are not valid litlen values, but they participate in the code construction):
| Litlen values | Codeword length |
|---|---|
| 0–143 | 8 |
| 144–255 | 9 |
| 256–279 | 7 |
| 280–287 | 8 |
The decompressor keeps those lengths in a table suitable for passing to huffman_decoder_init:
const uint8_t fixed_litlen_lengths[288] = {
/* 0 */ 8,
/* 1 */ 8,
...
/* 287 */ 8,
};
Back reference distances, ranging from 1 to 32,768, are encoded using a scheme similar to the one for lengths. The dist Huffman code encodes values between 0 and 29, each corresponding to a base length to which a number of extra bits are added to get the final distance:
| Dist | Extra Bits | Distance(s) |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 2 |
| 2 | 0 | 3 |
| 3 | 0 | 4 |
| 4 | 1 | 5–6 |
| 5 | 1 | 7–8 |
| 6 | 2 | 9–12 |
| 7 | 2 | 13–16 |
| 8 | 3 | 17–24 |
| 9 | 3 | 25–32 |
| 10 | 4 | 33–48 |
| 11 | 4 | 49–64 |
| 12 | 5 | 65–96 |
| 13 | 5 | 97–128 |
| 14 | 6 | 129–192 |
| 15 | 6 | 193–256 |
| 16 | 7 | 257–384 |
| 17 | 7 | 385–512 |
| 18 | 8 | 513–768 |
| 19 | 8 | 769–1024 |
| 20 | 9 | 1025–1536 |
| 21 | 9 | 1537–2048 |
| 22 | 10 | 2049–3072 |
| 23 | 10 | 3073–4096 |
| 24 | 11 | 4097–6144 |
| 25 | 11 | 6145–8192 |
| 26 | 12 | 8193–12288 |
| 27 | 12 | 12289–16384 |
| 28 | 13 | 16385–24576 |
| 29 | 13 | 24577–32768 |
The fixed dist code is a canonical Huffman code where all codewords are 5 bits long. Although trivial, the decompressor keeps it in a table so that it can be used with huffman_decoder_init (dist values 30–31 are not valid, but are specified as participating in the Huffman code construction, though they do not have any effect):
const uint8_t fixed_dist_lengths[32] = {
/* 0 */ 5,
/* 1 */ 5,
...
/* 31 */ 5,
};
The code for decompressing, or inflating, a fixed Huffman code deflate block is shown below.
static inf_stat_t inf_fixed_block(istream_t *is, uint8_t *dst,
size_t dst_cap, size_t *dst_pos)
{
huffman_decoder_t litlen_dec, dist_dec;
huffman_decoder_init(&litlen_dec, fixed_litlen_lengths,
sizeof(fixed_litlen_lengths) /
sizeof(fixed_litlen_lengths[0]));
huffman_decoder_init(&dist_dec, fixed_dist_lengths,
sizeof(fixed_dist_lengths) /
sizeof(fixed_dist_lengths[0]));
return inf_block(is, dst, dst_cap, dst_pos, &litlen_dec, &dist_dec);
}
#define LITLEN_EOB 256
#define LITLEN_MAX 285
#define LITLEN_TBL_OFFSET 257
#define MIN_LEN 3
#define MAX_LEN 258
#define DISTSYM_MAX 29
#define MIN_DISTANCE 1
#define MAX_DISTANCE 32768
static inf_stat_t inf_block(istream_t *is, uint8_t *dst, size_t dst_cap,
size_t *dst_pos,
const huffman_decoder_t *litlen_dec,
const huffman_decoder_t *dist_dec)
{
uint64_t bits;
size_t used, used_tot, dist, len;
int litlen, distsym;
uint16_t ebits;
while (true) {
/* Read a litlen symbol. */
bits = istream_bits(is);
litlen = huffman_decode(litlen_dec, (uint16_t)bits, &used);
bits >>= used;
used_tot = used;
if (litlen < 0 || litlen > LITLEN_MAX) {
/* Failed to decode, or invalid symbol. */
return HWINF_ERR;
} else if (litlen <= UINT8_MAX) {
/* Literal. */
if (!istream_advance(is, used_tot)) {
return HWINF_ERR;
}
if (*dst_pos == dst_cap) {
return HWINF_FULL;
}
lz77_output_lit(dst, (*dst_pos)++, (uint8_t)litlen);
continue;
} else if (litlen == LITLEN_EOB) {
/* End of block. */
if (!istream_advance(is, used_tot)) {
return HWINF_ERR;
}
return HWINF_OK;
}
/* It is a back reference. Figure out the length. */
assert(litlen >= LITLEN_TBL_OFFSET && litlen <= LITLEN_MAX);
len = litlen_tbl[litlen - LITLEN_TBL_OFFSET].base_len;
ebits = litlen_tbl[litlen - LITLEN_TBL_OFFSET].ebits;
if (ebits != 0) {
len += lsb(bits, ebits);
bits >>= ebits;
used_tot += ebits;
}
assert(len >= MIN_LEN && len <= MAX_LEN);
/* Get the distance. */
distsym = huffman_decode(dist_dec, (uint16_t)bits, &used);
bits >>= used;
used_tot += used;
if (distsym < 0 || distsym > DISTSYM_MAX) {
/* Failed to decode, or invalid symbol. */
return HWINF_ERR;
}
dist = dist_tbl[distsym].base_dist;
ebits = dist_tbl[distsym].ebits;
if (ebits != 0) {
dist += lsb(bits, ebits);
bits >>= ebits;
used_tot += ebits;
}
assert(dist >= MIN_DISTANCE && dist <= MAX_DISTANCE);
assert(used_tot <= ISTREAM_MIN_BITS);
if (!istream_advance(is, used_tot)) {
return HWINF_ERR;
}
/* Bounds check and output the backref. */
if (dist > *dst_pos) {
return HWINF_ERR;
}
if (round_up(len, 8) <= dst_cap - *dst_pos) {
lz77_output_backref64(dst, *dst_pos, dist, len);
} else if (len <= dst_cap - *dst_pos) {
lz77_output_backref(dst, *dst_pos, dist, len);
} else {
return HWINF_FULL;
}
(*dst_pos) += len;
}
}
Note that as an optimization when there is enough room in the output buffer, we output back references using the routine below which copies 64 bits at a time. It is "sloppy" in the sense that it often copies a few extra bytes (to the next multiple of 8), but it is much faster than lz77_output_backref since it needs fewer loop iterations and memory accesses. In fact, short back references will now all be handled by a single iteration, which is great for branch prediction.
/* Output the (dist,len) backref at dst_pos in dst using 64-bit wide writes.
There must be enough room for len bytes rounded to the next multiple of 8. */
static inline void lz77_output_backref64(uint8_t *dst, size_t dst_pos,
size_t dist, size_t len)
{
size_t i;
uint64_t tmp;
assert(len > 0);
assert(dist <= dst_pos && "cannot reference before beginning of dst");
if (len > dist) {
/* Self-overlapping backref; fall back to byte-by-byte copy. */
lz77_output_backref(dst, dst_pos, dist, len);
return;
}
i = 0;
do {
memcpy(&tmp, &dst[dst_pos - dist + i], 8);
memcpy(&dst[dst_pos + i], &tmp, 8);
i += 8;
} while (i < len);
}
Dynamic Huffman Code Deflate Blocks
Deflate blocks using dynamic Huffman codes work similarly to the blocks described above, but instead of using pre-determined Huffman codes for the litlen and dist codes, they use codes that are stored in the Deflate stream itself, at the start of the block. The name is perhaps unfortunate, since dynamic Huffman codes can also refer to codes that change during the coding process, sometimes called adaptive Huffman coding. The codes described here have nothing to do with that; they are only dynamic in the sense that different blocks can use different codes.
The encoding of the dynamic litlen and dist codes is the most intricate part of the Deflate format, but once the codes have been retrieved, decompression proceeds in the same way as for blocks in the previous section, using inf_block:
static inf_stat_t inf_dyn_block(istream_t *is, uint8_t *dst,
size_t dst_cap, size_t *dst_pos)
{
inf_stat_t s;
huffman_decoder_t litlen_dec, dist_dec;
s = init_dyn_decoders(is, &litlen_dec, &dist_dec);
if (s != HWINF_OK) {
return s;
}
return inf_block(is, dst, dst_cap, dst_pos, &litlen_dec, &dist_dec);
}
The litlen and dist codes for a dynamic Deflate block are stored as a series of codeword lengths. Those codeword lengths are themselves encoded using a third Huffman code, which we will call the codelen code. Finally, that code is itself defined by codeword lengths (codelen_lens) stored in the block. (Did I mention it was intricate?)
At the beginning of the dynamic block are 14 bits that define the number of litlen, dist, and codelen codeword lengths that should be read from the block:
#define MIN_CODELEN_LENS 4
#define MAX_CODELEN_LENS 19
#define MIN_LITLEN_LENS 257
#define MAX_LITLEN_LENS 288
#define MIN_DIST_LENS 1
#define MAX_DIST_LENS 32
#define CODELEN_MAX_LIT 15
#define CODELEN_COPY 16
#define CODELEN_COPY_MIN 3
#define CODELEN_COPY_MAX 6
#define CODELEN_ZEROS 17
#define CODELEN_ZEROS_MIN 3
#define CODELEN_ZEROS_MAX 10
#define CODELEN_ZEROS2 18
#define CODELEN_ZEROS2_MIN 11
#define CODELEN_ZEROS2_MAX 138
/* RFC 1951, 3.2.7 */
static const int codelen_lengths_order[MAX_CODELEN_LENS] =
{ 16, 17, 18, 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1, 15 };
static inf_stat_t init_dyn_decoders(istream_t *is,
huffman_decoder_t *litlen_dec,
huffman_decoder_t *dist_dec)
{
uint64_t bits;
size_t num_litlen_lens, num_dist_lens, num_codelen_lens;
uint8_t codelen_lengths[MAX_CODELEN_LENS];
uint8_t code_lengths[MAX_LITLEN_LENS + MAX_DIST_LENS];
size_t i, n, used;
int sym;
huffman_decoder_t codelen_dec;
bits = istream_bits(is);
/* Number of litlen codeword lengths (5 bits + 257). */
num_litlen_lens = (size_t)(lsb(bits, 5) + MIN_LITLEN_LENS);
bits >>= 5;
assert(num_litlen_lens <= MAX_LITLEN_LENS);
/* Number of dist codeword lengths (5 bits + 1). */
num_dist_lens = (size_t)(lsb(bits, 5) + MIN_DIST_LENS);
bits >>= 5;
assert(num_dist_lens <= MAX_DIST_LENS);
/* Number of code length lengths (4 bits + 4). */
num_codelen_lens = (size_t)(lsb(bits, 4) + MIN_CODELEN_LENS);
bits >>= 4;
assert(num_codelen_lens <= MAX_CODELEN_LENS);
if (!istream_advance(is, 5 + 5 + 4)) {
return HWINF_ERR;
}
After those bits follow the codeword lengths for the codelen code. The lengths are plain three-bit values, but they are written in a special order defined by codelen_lengths_order above. While there are 19 lengths to be specified, only num_codelen_lens will be read from the stream; the rest are implicitly zero. It is for this reason the lengths are in a special order: to increase the chance that latter lengths will all be zero and do not have to be stored in the block.
/* Read the codelen codeword lengths (3 bits each)
and initialize the codelen decoder. */
for (i = 0; i < num_codelen_lens; i++) {
bits = istream_bits(is);
codelen_lengths[codelen_lengths_order[i]] =
(uint8_t)lsb(bits, 3);
if (!istream_advance(is, 3)) {
return HWINF_ERR;
}
}
for (; i < MAX_CODELEN_LENS; i++) {
codelen_lengths[codelen_lengths_order[i]] = 0;
}
if (!huffman_decoder_init(&codelen_dec, codelen_lengths,
MAX_CODELEN_LENS)) {
return HWINF_ERR;
}
With the codelen decoder set up, we can proceed to read the litlen and dist codeword lengths from the stream.
/* Read the litlen and dist codeword lengths. */
i = 0;
while (i < num_litlen_lens + num_dist_lens) {
bits = istream_bits(is);
sym = huffman_decode(&codelen_dec, (uint16_t)bits, &used);
bits >>= used;
if (!istream_advance(is, used)) {
return HWINF_ERR;
}
if (sym >= 0 && sym <= CODELEN_MAX_LIT) {
/* A literal codeword length. */
code_lengths[i++] = (uint8_t)sym;
}
Lengths 16, 17, and 18 are not real lengths, but indicate that the previous length should be repeated some number of times, or that a zero length should be repeated:
else if (sym == CODELEN_COPY) {
/* Copy the previous codeword length 3--6 times. */
if (i < 1) {
return HWINF_ERR; /* No previous length. */
}
/* 2 bits + 3 */
n = (size_t)lsb(bits, 2) + CODELEN_COPY_MIN;
if (!istream_advance(is, 2)) {
return HWINF_ERR;
}
assert(n >= CODELEN_COPY_MIN && n <= CODELEN_COPY_MAX);
if (i + n > num_litlen_lens + num_dist_lens) {
return HWINF_ERR;
}
while (n--) {
code_lengths[i] = code_lengths[i - 1];
i++;
}
} else if (sym == CODELEN_ZEROS) {
/* 3--10 zeros; 3 bits + 3 */
n = (size_t)(lsb(bits, 3) + CODELEN_ZEROS_MIN);
if (!istream_advance(is, 3)) {
return HWINF_ERR;
}
assert(n >= CODELEN_ZEROS_MIN &&
n <= CODELEN_ZEROS_MAX);
if (i + n > num_litlen_lens + num_dist_lens) {
return HWINF_ERR;
}
while (n--) {
code_lengths[i++] = 0;
}
} else if (sym == CODELEN_ZEROS2) {
/* 11--138 zeros; 7 bits + 11. */
n = (size_t)(lsb(bits, 7) + CODELEN_ZEROS2_MIN);
if (!istream_advance(is, 7)) {
return HWINF_ERR;
}
assert(n >= CODELEN_ZEROS2_MIN &&
n <= CODELEN_ZEROS2_MAX);
if (i + n > num_litlen_lens + num_dist_lens) {
return HWINF_ERR;
}
while (n--) {
code_lengths[i++] = 0;
}
} else {
/* Invalid symbol. */
return HWINF_ERR;
}
}
Note that the litlen and dist lengths are read one after the other into the same code_lengths array. They could not be read separately, because code length runs can carry over from the last litlen lengths to the first dist lengths.
With the codeword lengths ready for use, we can set up the Huffman decoders and return to the task of decoding literals and back references:
if (!huffman_decoder_init(litlen_dec, &code_lengths[0],
num_litlen_lens)) {
return HWINF_ERR;
}
if (!huffman_decoder_init(dist_dec, &code_lengths[num_litlen_lens],
num_dist_lens)) {
return HWINF_ERR;
}
return HWINF_OK;
}
Compression (Deflation)
From the sections above, we have all the tools needed for Deflate compression: Lempel–Ziv, Huffman coding, bitstreams, and the description of the three Deflate block types. This section puts the pieces together to finally perform Deflate compression.
Lempel–Ziv compression parses the source data into a sequence of back references and literals. This sequence needs to be divided and encoded into Deflate blocks as described in the previous section. Choosing how to do this division is sometimes referred to as block splitting. On the one hand, each new block carries some overhead which varies depending on block type and contents, so fewer blocks means less overhead. On the other hand, the overhead from starting a new block might be worth it, for example if the characteristics of the data lead to a more efficient Huffman encoding in the new block and smaller output overall.
Block splitting is a difficult optimization problem. Some compressors (such as Zopfli) try harder than others, but most just use a greedy approach: output a block once a certain size has been reached.
The different block types impose different size constraints:
- Uncompressed blocks can contain at most 65,535 bytes.
- Fixed Huffman Code blocks do not have a maximum size.
- Dynamic Huffman Code blocks do not generally have a maximum size, but because our implementation of Huffman's algorithm uses 16-bit symbol frequencies, we are limited to at most 65,535 symbols.
To be able to freely choose any of the three types for block, we limit the block size to at most 65,534 bytes:
/* The largest number of bytes that will fit in any kind of block is 65,534.
It will fit in an uncompressed block (max 65,535 bytes) and a Huffman
block with only literals (65,535 symbols including end-of-block marker). */
#define MAX_BLOCK_LEN_BYTES 65534
We use a structure to keep track of the output bitstream and the contents of the current block during deflation:
typedef struct deflate_state_t deflate_state_t;
struct deflate_state_t {
ostream_t os;
const uint8_t *block_src; /* First src byte in the block. */
size_t block_len; /* Number of symbols in the current block. */
size_t block_len_bytes; /* Number of src bytes in the block. */
/* Symbol frequencies for the current block. */
uint16_t litlen_freqs[LITLEN_MAX + 1];
uint16_t dist_freqs[DISTSYM_MAX + 1];
struct {
uint16_t distance; /* Backref distance. */
union {
uint16_t lit; /* Literal byte or end-of-block. */
uint16_t len; /* Backref length (distance != 0). */
} u;
} block[MAX_BLOCK_LEN_BYTES + 1];
};
static void reset_block(deflate_state_t *s)
{
s->block_len = 0;
s->block_len_bytes = 0;
memset(s->litlen_freqs, 0, sizeof(s->litlen_freqs));
memset(s->dist_freqs, 0, sizeof(s->dist_freqs));
}
Callback functions are used to update the block with the output from lz77_compress, and write the block to the bitstream when it reaches the maximum size:
static bool lit_callback(uint8_t lit, void *aux)
{
deflate_state_t *s = aux;
if (s->block_len_bytes + 1 > MAX_BLOCK_LEN_BYTES) {
if (!write_block(s, false)) {
return false;
}
s->block_src += s->block_len_bytes;
reset_block(s);
}
assert(s->block_len < sizeof(s->block) / sizeof(s->block[0]));
s->block[s->block_len ].distance = 0;
s->block[s->block_len++].u.lit = lit;
s->block_len_bytes++;
s->litlen_freqs[lit]++;
return true;
}
static uint8_t distance2dist(size_t distance)
{
assert(distance >= 1 && distance <= MAX_DISTANCE);
return (distance <= 256) ? distance2dist_lo[(distance - 1)]
: distance2dist_hi[(distance - 1) >> 7];
}
/* Mapping from length (3--258) to litlen symbol (257--285). */
extern const uint16_t len2litlen[259];
static bool backref_callback(size_t dist, size_t len, void *aux)
{
deflate_state_t *s = aux;
if (s->block_len_bytes + len > MAX_BLOCK_LEN_BYTES) {
if (!write_block(s, false)) {
return false;
}
s->block_src += s->block_len_bytes;
reset_block(s);
}
assert(s->block_len < sizeof(s->block) / sizeof(s->block[0]));
s->block[s->block_len ].distance = (uint16_t)dist;
s->block[s->block_len++].u.len = (uint16_t)len;
s->block_len_bytes += len;
assert(len >= MIN_LEN && len <= MAX_LEN);
assert(dist >= MIN_DISTANCE && dist <= MAX_DISTANCE);
s->litlen_freqs[len2litlen[len]]++;
s->dist_freqs[distance2dist(dist)]++;
return true;
}
The interesting part is of course writing the blocks. Writing an uncompressed block is straight-forward:
static bool write_uncomp_block(deflate_state_t *s, bool final)
{
uint8_t len_nlen[4];
/* Write the block header. */
if (!ostream_write(&s->os, (0x0 << 1) | final, 3)) {
return false;
}
len_nlen[0] = (uint8_t)(s->block_len_bytes >> 0);
len_nlen[1] = (uint8_t)(s->block_len_bytes >> 8);
len_nlen[2] = ~len_nlen[0];
len_nlen[3] = ~len_nlen[1];
if (!ostream_write_bytes_aligned(&s->os, len_nlen, sizeof(len_nlen))) {
return false;
}
if (!ostream_write_bytes_aligned(&s->os, s->block_src,
s->block_len_bytes)) {
return false;
}
return true;
}
To write a static Huffman block, we first generate canonical Huffman codes based on the fixed codeword lengths for the litlen and dist codes. Then we iterate through the block, writing the symbols using those codes:
static bool write_static_block(deflate_state_t *s, bool final)
{
huffman_encoder_t litlen_enc, dist_enc;
/* Write the block header. */
if (!ostream_write(&s->os, (0x1 << 1) | final, 3)) {
return false;
}
huffman_encoder_init2(&litlen_enc, fixed_litlen_lengths,
sizeof(fixed_litlen_lengths) /
sizeof(fixed_litlen_lengths[0]));
huffman_encoder_init2(&dist_enc, fixed_dist_lengths,
sizeof(fixed_dist_lengths) /
sizeof(fixed_dist_lengths[0]));
return write_huffman_block(s, &litlen_enc, &dist_enc);
}
static bool write_huffman_block(deflate_state_t *s,
const huffman_encoder_t *litlen_enc,
const huffman_encoder_t *dist_enc)
{
size_t i, nbits;
uint16_t distance, dist, len, litlen;
uint64_t bits, ebits;
for (i = 0; i < s->block_len; i++) {
if (s->block[i].distance == 0) {
/* Literal or EOB. */
litlen = s->block[i].u.lit;
assert(litlen <= LITLEN_EOB);
if (!ostream_write(&s->os,
litlen_enc->codewords[litlen],
litlen_enc->lengths[litlen])) {
return false;
}
continue;
}
/* Back reference length. */
len = s->block[i].u.len;
litlen = len2litlen[len];
/* litlen bits */
bits = litlen_enc->codewords[litlen];
nbits = litlen_enc->lengths[litlen];
/* ebits */
ebits = len - litlen_tbl[litlen - LITLEN_TBL_OFFSET].base_len;
bits |= ebits << nbits;
nbits += litlen_tbl[litlen - LITLEN_TBL_OFFSET].ebits;
/* Back reference distance. */
distance = s->block[i].distance;
dist = distance2dist(distance);
/* dist bits */
bits |= (uint64_t)dist_enc->codewords[dist] << nbits;
nbits += dist_enc->lengths[dist];
/* ebits */
ebits = distance - dist_tbl[dist].base_dist;
bits |= ebits << nbits;
nbits += dist_tbl[dist].ebits;
if (!ostream_write(&s->os, bits, nbits)) {
return false;
}
}
return true;
}
Dynamic Huffman blocks are of course the trickiest to write, since they include the intricate encoding of the litlen and dist codes. We will use this struct to represent their encoding:
typedef struct codelen_sym_t codelen_sym_t;
struct codelen_sym_t {
uint8_t sym;
uint8_t count; /* For symbols 16, 17, 18. */
};
First, we drop trailing zero litlen and dist codeword lengths, and copy them into a common array for encoding. We cannot drop all trailing zeros: it is not possible to encode a Deflate block with fewer than one dist code. (It is also not possible to have fewer then 257 litlen codes, but since there is always an end-of-byte marker, there will always be a non-zero code length for symbol 256.)
/* Encode litlen_lens and dist_lens into encoded. *num_litlen_lens and
*num_dist_lens will be set to the number of encoded litlen and dist lens,
respectively. Returns the number of elements in encoded. */
static size_t encode_dist_litlen_lens(const uint8_t *litlen_lens,
const uint8_t *dist_lens,
codelen_sym_t *encoded,
size_t *num_litlen_lens,
size_t *num_dist_lens)
{
size_t i, n;
uint8_t lens[LITLEN_MAX + 1 + DISTSYM_MAX + 1];
*num_litlen_lens = LITLEN_MAX + 1;
*num_dist_lens = DISTSYM_MAX + 1;
/* Drop trailing zero litlen lengths. */
assert(litlen_lens[LITLEN_EOB] != 0 && "EOB len should be non-zero.");
while (litlen_lens[*num_litlen_lens - 1] == 0) {
(*num_litlen_lens)--;
}
assert(*num_litlen_lens >= MIN_LITLEN_LENS);
/* Drop trailing zero dist lengths, keeping at least one. */
while (dist_lens[*num_dist_lens - 1] == 0 && *num_dist_lens > 1) {
(*num_dist_lens)--;
}
assert(*num_dist_lens >= MIN_DIST_LENS);
/* Copy the lengths into a unified array. */
n = 0;
for (i = 0; i < *num_litlen_lens; i++) {
lens[n++] = litlen_lens[i];
}
for (i = 0; i < *num_dist_lens; i++) {
lens[n++] = dist_lens[i];
}
return encode_lens(lens, n, encoded);
}
Once the code lengths are in a single array, we perform the encoding, using special symbols for runs of identical code lengths.
/* Encode the n code lengths in lens into encoded, returning the number of
elements in encoded. */
static size_t encode_lens(const uint8_t *lens, size_t n, codelen_sym_t *encoded)
{
size_t i, j, num_encoded;
uint8_t count;
i = 0;
num_encoded = 0;
while (i < n) {
if (lens[i] == 0) {
/* Scan past the end of this zero run (max 138). */
for (j = i; j < min(n, i + CODELEN_ZEROS2_MAX) &&
lens[j] == 0; j++);
count = (uint8_t)(j - i);
if (count < CODELEN_ZEROS_MIN) {
/* Output a single zero. */
encoded[num_encoded++].sym = 0;
i++;
continue;
}
/* Output a repeated zero. */
if (count <= CODELEN_ZEROS_MAX) {
/* Repeated zero 3--10 times. */
assert(count >= CODELEN_ZEROS_MIN &&
count <= CODELEN_ZEROS_MAX);
encoded[num_encoded].sym = CODELEN_ZEROS;
encoded[num_encoded++].count = count;
} else {
/* Repeated zero 11--138 times. */
assert(count >= CODELEN_ZEROS2_MIN &&
count <= CODELEN_ZEROS2_MAX);
encoded[num_encoded].sym = CODELEN_ZEROS2;
encoded[num_encoded++].count = count;
}
i = j;
continue;
}
/* Output len. */
encoded[num_encoded++].sym = lens[i++];
/* Scan past the end of the run of this len (max 6). */
for (j = i; j < min(n, i + CODELEN_COPY_MAX) &&
lens[j] == lens[i - 1]; j++);
count = (uint8_t)(j - i);
if (count >= CODELEN_COPY_MIN) {
/* Repeat last len 3--6 times. */
assert(count >= CODELEN_COPY_MIN &&
count <= CODELEN_COPY_MAX);
encoded[num_encoded].sym = CODELEN_COPY;
encoded[num_encoded++].count = count;
i = j;
continue;
}
}
return num_encoded;
}
The symbols used in the encoding above will in turn get written using a Huffman code, the "codelen code". The codeword lengths of the codelen code are written to the block in a certain order, with lengths more likely to be zero coming last. A function is used to count how many of the lengths that need to be written:
static const int codelen_lengths_order[19] =
{ 16, 17, 18, 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1, 15 };
/* Count the number of significant (not trailing zeros) codelen lengths. */
size_t count_codelen_lens(const uint8_t *codelen_lens)
{
size_t n = MAX_CODELEN_LENS;
/* Drop trailing zero lengths. */
while (codelen_lens[codelen_lengths_order[n - 1]] == 0) {
n--;
}
/* The first 4 lengths in the order (16, 17, 18, 0) cannot be used to
encode any non-zero lengths. Since there will always be at least
one non-zero codeword length (for EOB), n will be >= 4. */
assert(n >= MIN_CODELEN_LENS && n <= MAX_CODELEN_LENS);
return n;
}
Assuming we have the litlen and dist codes set up, the encoding of their codeword lengths, and the code for that encoding, we can write the dynamic Huffman block:
static bool write_dynamic_block(deflate_state_t *s, bool final,
size_t num_litlen_lens, size_t num_dist_lens,
size_t num_codelen_lens,
const huffman_encoder_t *codelen_enc,
const codelen_sym_t *encoded_lens,
size_t num_encoded_lens,
const huffman_encoder_t *litlen_enc,
const huffman_encoder_t *dist_enc)
{
size_t i;
uint8_t codelen, sym;
size_t nbits;
uint64_t bits, hlit, hdist, hclen, count;
/* Block header. */
bits = (0x2 << 1) | final;
nbits = 3;
/* hlit (5 bits) */
hlit = num_litlen_lens - MIN_LITLEN_LENS;
bits |= hlit << nbits;
nbits += 5;
/* hdist (5 bits) */
hdist = num_dist_lens - MIN_DIST_LENS;
bits |= hdist << nbits;
nbits += 5;
/* hclen (4 bits) */
hclen = num_codelen_lens - MIN_CODELEN_LENS;
bits |= hclen << nbits;
nbits += 4;
if (!ostream_write(&s->os, bits, nbits)) {
return false;
}
/* Codelen lengths. */
for (i = 0; i < num_codelen_lens; i++) {
codelen = codelen_enc->lengths[codelen_lengths_order[i]];
if (!ostream_write(&s->os, codelen, 3)) {
return false;
}
}
/* Litlen and dist code lengths. */
for (i = 0; i < num_encoded_lens; i++) {
sym = encoded_lens[i].sym;
bits = codelen_enc->codewords[sym];
nbits = codelen_enc->lengths[sym];
count = encoded_lens[i].count;
if (sym == CODELEN_COPY) { /* 2 ebits */
bits |= (count - CODELEN_COPY_MIN) << nbits;
nbits += 2;
} else if (sym == CODELEN_ZEROS) { /* 3 ebits */
bits |= (count - CODELEN_ZEROS_MIN) << nbits;
nbits += 3;
} else if (sym == CODELEN_ZEROS2) { /* 7 ebits */
bits |= (count - CODELEN_ZEROS2_MIN) << nbits;
nbits += 7;
}
if (!ostream_write(&s->os, bits, nbits)) {
return false;
}
}
return write_huffman_block(s, litlen_enc, dist_enc);
}
For each block, we want to use the type that needs the smallest number of bits. For an uncompressed block, the length can be computed quickly:
/* Calculate the number of bits for an uncompressed block, including header. */
static size_t uncomp_block_len(const deflate_state_t *s)
{
size_t bit_pos, padding;
/* Bit position after writing the block header. */
bit_pos = ostream_bit_pos(&s->os) + 3;
padding = round_up(bit_pos, 8) - bit_pos;
/* Header + padding + len/nlen + block contents. */
return 3 + padding + 2 * 16 + s->block_len_bytes * 8;
}
For Huffman encoded blocks, we can compute the length of the body using the litlen and dist symbol frequencies and codeword lengths:
/* Calculate the number of bits for a Huffman encoded block body. */
static size_t huffman_block_body_len(const deflate_state_t *s,
const uint8_t *litlen_lens,
const uint8_t *dist_lens)
{
size_t i, freq, len;
len = 0;
for (i = 0; i <= LITLEN_MAX; i++) {
freq = s->litlen_freqs[i];
len += litlen_lens[i] * freq;
if (i >= LITLEN_TBL_OFFSET) {
len += litlen_tbl[i - LITLEN_TBL_OFFSET].ebits * freq;
}
}
for (i = 0; i <= DISTSYM_MAX; i++) {
freq = s->dist_freqs[i];
len += dist_lens[i] * freq;
len += dist_tbl[i].ebits * freq;
}
return len;
}
For a static block, the total length is 3 bits for the header plus the length of the body. For a dynamic block, computing the size of the header requires a bit more work:
/* Calculate the number of bits for a dynamic Huffman block. */
static size_t dyn_block_len(const deflate_state_t *s, size_t num_codelen_lens,
const uint16_t *codelen_freqs,
const huffman_encoder_t *codelen_enc,
const huffman_encoder_t *litlen_enc,
const huffman_encoder_t *dist_enc)
{
size_t len, i, freq;
/* Block header. */
len = 3;
/* Nbr of litlen, dist, and codelen lengths. */
len += 5 + 5 + 4;
/* Codelen lengths. */
len += 3 * num_codelen_lens;
/* Codelen encoding. */
for (i = 0; i < MAX_CODELEN_LENS; i++) {
freq = codelen_freqs[i];
len += codelen_enc->lengths[i] * freq;
/* Extra bits. */
if (i == CODELEN_COPY) {
len += 2 * freq;
} else if (i == CODELEN_ZEROS) {
len += 3 * freq;
} else if (i == CODELEN_ZEROS2) {
len += 7 * freq;
}
}
return len + huffman_block_body_len(s, litlen_enc->lengths,
dist_enc->lengths);
}
With all this in place, we can write the master block writing function:
/* Write the current deflate block, marking it final if that parameter is true,
returning false if there is not enough room in the output stream. */
static bool write_block(deflate_state_t *s, bool final)
{
size_t old_bit_pos, uncomp_len, static_len, dynamic_len;
huffman_encoder_t dyn_litlen_enc, dyn_dist_enc, codelen_enc;
size_t num_encoded_lens, num_litlen_lens, num_dist_lens;
codelen_sym_t encoded_lens[LITLEN_MAX + 1 + DISTSYM_MAX + 1];
uint16_t codelen_freqs[MAX_CODELEN_LENS] = {0};
size_t num_codelen_lens;
size_t i;
old_bit_pos = ostream_bit_pos(&s->os);
/* Add the end-of-block marker in case we write a Huffman block. */
assert(s->block_len < sizeof(s->block) / sizeof(s->block[0]));
assert(s->litlen_freqs[LITLEN_EOB] == 0);
s->block[s->block_len ].distance = 0;
s->block[s->block_len++].u.lit = LITLEN_EOB;
s->litlen_freqs[LITLEN_EOB] = 1;
uncomp_len = uncomp_block_len(s);
static_len = 3 + huffman_block_body_len(s, fixed_litlen_lengths,
fixed_dist_lengths);
/* Compute "dynamic" Huffman codes. */
huffman_encoder_init(&dyn_litlen_enc, s->litlen_freqs,
LITLEN_MAX + 1, 15);
huffman_encoder_init(&dyn_dist_enc, s->dist_freqs, DISTSYM_MAX + 1, 15);
tweak_dist_encoder(&dyn_dist_enc);
/* Encode the litlen and dist code lengths. */
num_encoded_lens = encode_dist_litlen_lens(dyn_litlen_enc.lengths,
dyn_dist_enc.lengths,
encoded_lens,
&num_litlen_lens,
&num_dist_lens);
/* Compute the codelen code. */
for (i = 0; i < num_encoded_lens; i++) {
codelen_freqs[encoded_lens[i].sym]++;
}
huffman_encoder_init(&codelen_enc, codelen_freqs, MAX_CODELEN_LENS, 7);
num_codelen_lens = count_codelen_lens(codelen_enc.lengths);
dynamic_len = dyn_block_len(s, num_codelen_lens, codelen_freqs,
&codelen_enc, &dyn_litlen_enc,
&dyn_dist_enc);
if (uncomp_len <= dynamic_len && uncomp_len <= static_len) {
if (!write_uncomp_block(s, final)) {
return false;
}
assert(ostream_bit_pos(&s->os) - old_bit_pos == uncomp_len);
} else if (static_len <= dynamic_len) {
if (!write_static_block(s, final)) {
return false;
}
assert(ostream_bit_pos(&s->os) - old_bit_pos == static_len);
} else {
if (!write_dynamic_block(s, final, num_litlen_lens,
num_dist_lens, num_codelen_lens,
&codelen_enc, encoded_lens,
num_encoded_lens, &dyn_litlen_enc,
&dyn_dist_enc)) {
return false;
}
assert(ostream_bit_pos(&s->os) - old_bit_pos == dynamic_len);
}
(void)old_bit_pos;
return true;
}
Finally, the driver of the whole deflation process simply has to set up the initial state, kick off the Lempel–Ziv compression, and write the final block:
/* Compress (deflate) the data in src into dst. The number of bytes output, at
most dst_cap, is stored in *dst_used. Returns false if there is not enough
room in dst. src and dst must not overlap. */
bool hwdeflate(const uint8_t *src, size_t src_len,
uint8_t *dst, size_t dst_cap, size_t *dst_used)
{
deflate_state_t s;
ostream_init(&s.os, dst, dst_cap);
reset_block(&s);
s.block_src = src;
if (!lz77_compress(src, src_len, &lit_callback,
&backref_callback, &s)) {
return false;
}
if (!write_block(&s, true)) {
return false;
}
/* The end of the final block should match the end of src. */
assert(s.block_src + s.block_len_bytes == src + src_len);
*dst_used = ostream_bytes_written(&s.os);
return true;
}
The Zip File Format
We have seen above exactly how the Deflate compression used in Zip files works, but what about the file format itself? This section explains it in detail and provides an implementation. The code is available in zip.h and zip.c.
Overview
The file format is described in PKZip's Application Note:
- Each file, or archive member, in the Zip file has a Local File Header with metadata about the member, such as its filename etc.
- The Central Directory serves as an index of the archive. It contains a Central File Header for each archive member and holds a copy of the metadata from the Local File Header, and more information such as the member's offset in the Zip file.
- At the end of the file, directly after the Central Directory, comes the End of Central Directory Record. This contains the size and position of the Central Directory, and an optional comment about the whole archive. It is the starting point for reading a Zip file.
Each archive member is compressed and stored individually. This means that even if there are similarities between files in the archive, those similarities are not exploited to generate better compression.
Having the Central Directory at the end enables an archive to be created gradually. As each member file is compressed, it gets written to the archive, and the index is written afterwards when all the compressed sizes, and therefore the file offsets, are known. A file can also be added to an existing archive fairly easily, by putting it after the last member and re-writing the Central Directory.
The ability to create archives gradually was especially important for archives spanning multiple floppy disks, or volumes. As compression progressed, PKZip would prompt the user to insert new floppies, and finally write the Central Directory to the last one(s). To extract a multi-volume archive, PKZip would first ask for the last floppy in order to read the Central Directory, and then for whatever floppies were needed to extract the requested files.
Perhaps surprisingly, there is no rule against having multiple files with the same name in an archive. This can lead to great confusion during file extraction: if there are multiple files with the specified name, which one should be extracted? Such confusion can turn into security problems. In the Android "Master Key" Bug (CVE-2013-4787, Black Hat slides / video), this allowed malicious actors to bypass the operating system's cryptographic signature checks when installing programs. Android programs are distributed in APK files, which are essentially Zip files. As it turned out, if an APK contained multiple files with the same name, the signature checking code would pick the last file with that name, whereas the installation code would pick the first file, meaning its signature was never checked. In other words, this minor difference between two Zip libraries made it possible to bypass the entire security model of the operating system.
Unlike most file formats, Zip files are not required to start with a signature or magic number. In fact, it is not specified that a Zip file must start in any particular way at all, making it easy to create a file which is both a valid Zip file and a valid file of another format at the same time, a so called polyglot file. For example, a self-extracting Zip file (such as pkz204g.exe) is usually both a valid executable and a Zip file: the first part is an executable, and after that follows the Zip file (which the executable extracts). The operating system can run it as an executable, but a Zip program will open it as a Zip file. This ability for Zip files to also be valid executables may have been the motivation for not requiring a signature at the beginning of the file.
While the self-extracting Zip/executable files are clever, polyglots can also cause security problems, as they may trick software that tries to determine the contents of a file, or allow delivering malicious code along with a file of a different type. For example, GIFARs, files that are both valid GIF images and Java Archives (JARs, a form of Zip file), have been used in security exploits on the web. For more thoughts on these kinds of problems, see Ange Albertini's Abusing file formats article (begins on page 18).
As we will see below, Zip files use 32-bit fields for offsets and sizes, limiting the size of the archive and its members to 4 GB. In Version 4.5 of the Application Note, PKWare added format extensions to allow 64-bit offsets and sizes. Files using those extensions are said to be in Zip64 format, but that is not covered in this article.
Data Structures
End of Central Directory Record
The EOCDR is normally used as the starting point for reading a Zip file. It contains the location and size of the Central Directory, and an optional comment about the whole archive.
For Zip files spanning multiple floppy disks, or volumes, the EOCDR also contains information about which disk we are currently on, on what disk the Central Directory begins, etc. This functionality is rarely used these days, and the code in this article does not handle such files.
The EOCDR is identified by the signature 'P' 'K', followed by the bytes 5 and 6. It then has the following structure, with integers stored in little-endian byte order:
/* End of Central Directory Record. */
struct eocdr {
uint16_t disk_nbr; /* Number of this disk. */
uint16_t cd_start_disk; /* Nbr. of disk with start of the CD. */
uint16_t disk_cd_entries; /* Nbr. of CD entries on this disk. */
uint16_t cd_entries; /* Nbr. of Central Directory entries. */
uint32_t cd_size; /* Central Directory size in bytes. */
uint32_t cd_offset; /* Central Directory file offset. */
uint16_t comment_len; /* Archive comment length. */
const uint8_t *comment; /* Archive comment. */
};
The EOCDR should be located at the end of the file. However, since it can have a trailing comment of arbitrary 16-bit length, we may have to search to find the exact position:
/* Read 16/32 bits little-endian and bump p forward afterwards. */
#define READ16(p) ((p) += 2, read16le((p) - 2))
#define READ32(p) ((p) += 4, read32le((p) - 4))
/* Size of the End of Central Directory Record, not including comment. */
#define EOCDR_BASE_SZ 22
#define EOCDR_SIGNATURE 0x06054b50 /* "PK\5\6" little-endian. */
#define MAX_BACK_OFFSET (1024 * 100)
static bool find_eocdr(struct eocdr *r, const uint8_t *src, size_t src_len)
{
size_t back_offset;
const uint8_t *p;
uint32_t signature;
for (back_offset = 0; back_offset <= MAX_BACK_OFFSET; back_offset++) {
if (src_len < EOCDR_BASE_SZ + back_offset) {
break;
}
p = &src[src_len - EOCDR_BASE_SZ - back_offset];
signature = READ32(p);
if (signature == EOCDR_SIGNATURE) {
r->disk_nbr = READ16(p);
r->cd_start_disk = READ16(p);
r->disk_cd_entries = READ16(p);
r->cd_entries = READ16(p);
r->cd_size = READ32(p);
r->cd_offset = READ32(p);
r->comment_len = READ16(p);
r->comment = p;
assert(p == &src[src_len - back_offset] &&
"All fields read.");
if (r->comment_len > back_offset) {
return false;
}
return true;
}
}
return false;
}
Writing an EOCDR is straight-forward. The function below does that and returns the number of bytes written.
/* Write 16/32 bits little-endian and bump p forward afterwards. */
#define WRITE16(p, x) (write16le((p), (x)), (p) += 2)
#define WRITE32(p, x) (write32le((p), (x)), (p) += 4)
static size_t write_eocdr(uint8_t *dst, const struct eocdr *r)
{
uint8_t *p = dst;
WRITE32(p, EOCDR_SIGNATURE);
WRITE16(p, r->disk_nbr);
WRITE16(p, r->cd_start_disk);
WRITE16(p, r->disk_cd_entries);
WRITE16(p, r->cd_entries);
WRITE32(p, r->cd_size);
WRITE32(p, r->cd_offset);
WRITE16(p, r->comment_len);
assert(p - dst == EOCDR_BASE_SZ);
if (r->comment_len != 0) {
memcpy(p, r->comment, r->comment_len);
p += r->comment_len;
}
return (size_t)(p - dst);
}
Central File Header
The Central Directory consists of Central File Headers written back-to-back, one for each member of the archive. Each header starts with the signature 'P', 'K', 1, 2, and then has the following structure:
#define EXT_ATTR_DIR (1U << 4)
#define EXT_ATTR_ARC (1U << 5)
/* Central File Header (Central Directory Entry) */
struct cfh {
uint16_t made_by_ver; /* Version made by. */
uint16_t extract_ver; /* Version needed to extract. */
uint16_t gp_flag; /* General-purpose bit flag. */
uint16_t method; /* Compression method. */
uint16_t mod_time; /* Modification time. */
uint16_t mod_date; /* Modification date. */
uint32_t crc32; /* CRC-32 checksum. */
uint32_t comp_size; /* Compressed size. */
uint32_t uncomp_size; /* Uncompressed size. */
uint16_t name_len; /* Filename length. */
uint16_t extra_len; /* Extra data length. */
uint16_t comment_len; /* Comment length. */
uint16_t disk_nbr_start; /* Disk nbr. where file begins. */
uint16_t int_attrs; /* Internal file attributes. */
uint32_t ext_attrs; /* External file attributes. */
uint32_t lfh_offset; /* Local File Header offset. */
const uint8_t *name; /* Filename. */
const uint8_t *extra; /* Extra data. */
const uint8_t *comment; /* File comment. */
};
made_by_ver and extract_ver encode operating system and version information of the program used to add this member, and what version is required to extract it, respectively. The most significant eight bits encode the operating system (for example, 0 means DOS, 3 Unix, 10 Windows NTFS) and the lower eight bits the software version. We will set that version to decimal 20, indicating compatibility with PKZip 2.0.
gp_flag contains various flags. Some interesting ones are bit 0, which indicates whether the member is encrypted (out of scope for this article), and bits 1 and 2 which encode the Deflate compression level (0 for normal, 1 for maximum, 2 for fast, 3 for super fast).
method encodes the compression method. Method 0 means the data is uncompressed, method 8 means it is deflated. Other values refer to historic or newer algorithms, but almost all Zip files use only these two values.
mod_time and mod_date contain the file's modification date and time, encoded in MS-DOS date/time format. We use the code below to convert to and from regular C time_t timestamps.
/* Convert DOS date and time to time_t. */
static time_t dos2ctime(uint16_t dos_date, uint16_t dos_time)
{
struct tm tm = {0};
tm.tm_sec = (dos_time & 0x1f) * 2; /* Bits 0--4: Secs divided by 2. */
tm.tm_min = (dos_time >> 5) & 0x3f; /* Bits 5--10: Minute. */
tm.tm_hour = (dos_time >> 11); /* Bits 11-15: Hour (0--23). */
tm.tm_mday = (dos_date & 0x1f); /* Bits 0--4: Day (1--31). */
tm.tm_mon = ((dos_date >> 5) & 0xf) - 1; /* Bits 5--8: Month (1--12). */
tm.tm_year = (dos_date >> 9) + 80; /* Bits 9--15: Year-1980. */
tm.tm_isdst = -1;
return mktime(&tm);
}
/* Convert time_t to DOS date and time. */
static void ctime2dos(time_t t, uint16_t *dos_date, uint16_t *dos_time)
{
struct tm *tm = localtime(&t);
/* Clamp the year to the representable range: 1980 to 2107. */
if (tm->tm_year + 1900 < 1980) {
tm->tm_year = 1980 - 1900;
} else if (tm->tm_year + 1900 > 2107) {
tm->tm_year = 2107 - 1900;
}
*dos_time = 0;
*dos_time |= tm->tm_sec / 2; /* Bits 0--4: Second divided by two. */
*dos_time |= tm->tm_min << 5; /* Bits 5--10: Minute. */
*dos_time |= tm->tm_hour << 11; /* Bits 11-15: Hour. */
*dos_date = 0;
*dos_date |= tm->tm_mday; /* Bits 0--4: Day (1--31). */
*dos_date |= (tm->tm_mon + 1) << 5; /* Bits 5--8: Month (1--12). */
*dos_date |= (tm->tm_year - 80) << 9; /* Bits 9--15: Year from 1980. */
}
The crc32 field contains a cyclic redundancy check value of the uncompressed data. This is used to verify the intergity of the data after extraction. See crc32.c for an implementation.
comp_size and uncomp_size contain the compressed and uncompressed size of the member file's data, respectively. The next three fields contain the lengths of the name, comment, and extra data that follow immediately after the header. disk_nbr_start is for archives spanning multiple floppy disks.
int_attrs and ext_attrs describe internal and external attributes of the file. Internal attributes pertain to the contents of the file, such as the lowest bit which indicates that it only contains text. The external attributes are such as whether the file is read-only, hidden, etc. The encoding of this field varies by operating system, that is, it depends on made_by_ver. On DOS, the lowest 8 bits contain the file's attributes byte that one would get from an Int 21/AX=4300h system call. For example, bit 4 means it is a directory and bit 5 means the "archive" attribute is set (which is true for most files on DOS). From what I understand, those bits will be set similarly on other operating systems for compatibility. On Unix, the upper 16 bits of this field hold the file mode bits, as returned by stat(2) in st_mode.
lfh_offset tells us where to find the file's Local File Header, name is the filename (not null terminated), and comment is an optional comment for this archive member (not null terminated). extra can hold optional extra data such as Unix file ownership information, higher resolution modification date and time, or Zip64 fields.
The functions below are used to read and write CFHs.
/* Size of a Central File Header, not including name, extra, and comment. */
#define CFH_BASE_SZ 46
#define CFH_SIGNATURE 0x02014b50 /* "PK\1\2" little-endian. */
static bool read_cfh(struct cfh *cfh, const uint8_t *src, size_t src_len,
size_t offset)
{
const uint8_t *p;
uint32_t signature;
if (offset > src_len || src_len - offset < CFH_BASE_SZ) {
return false;
}
p = &src[offset];
signature = READ32(p);
if (signature != CFH_SIGNATURE) {
return false;
}
cfh->made_by_ver = READ16(p);
cfh->extract_ver = READ16(p);
cfh->gp_flag = READ16(p);
cfh->method = READ16(p);
cfh->mod_time = READ16(p);
cfh->mod_date = READ16(p);
cfh->crc32 = READ32(p);
cfh->comp_size = READ32(p);
cfh->uncomp_size = READ32(p);
cfh->name_len = READ16(p);
cfh->extra_len = READ16(p);
cfh->comment_len = READ16(p);
cfh->disk_nbr_start = READ16(p);
cfh->int_attrs = READ16(p);
cfh->ext_attrs = READ32(p);
cfh->lfh_offset = READ32(p);
cfh->name = p;
cfh->extra = cfh->name + cfh->name_len;
cfh->comment = cfh->extra + cfh->extra_len;
assert(p == &src[offset + CFH_BASE_SZ] && "All fields read.");
if (src_len - offset - CFH_BASE_SZ <
(size_t)cfh->name_len + cfh->extra_len + cfh->comment_len) {
return false;
}
return true;
}
static size_t write_cfh(uint8_t *dst, const struct cfh *cfh)
{
uint8_t *p = dst;
WRITE32(p, CFH_SIGNATURE);
WRITE16(p, cfh->made_by_ver);
WRITE16(p, cfh->extract_ver);
WRITE16(p, cfh->gp_flag);
WRITE16(p, cfh->method);
WRITE16(p, cfh->mod_time);
WRITE16(p, cfh->mod_date);
WRITE32(p, cfh->crc32);
WRITE32(p, cfh->comp_size);
WRITE32(p, cfh->uncomp_size);
WRITE16(p, cfh->name_len);
WRITE16(p, cfh->extra_len);
WRITE16(p, cfh->comment_len);
WRITE16(p, cfh->disk_nbr_start);
WRITE16(p, cfh->int_attrs);
WRITE32(p, cfh->ext_attrs);
WRITE32(p, cfh->lfh_offset);
assert(p - dst == CFH_BASE_SZ);
if (cfh->name_len != 0) {
memcpy(p, cfh->name, cfh->name_len);
p += cfh->name_len;
}
if (cfh->extra_len != 0) {
memcpy(p, cfh->extra, cfh->extra_len);
p += cfh->extra_len;
}
if (cfh->comment_len != 0) {
memcpy(p, cfh->comment, cfh->comment_len);
p += cfh->comment_len;
}
return (size_t)(p - dst);
}
Local File Header
The data of each archive member is preceded by a Local File Header, which repeats most of the information from the Central File Header.
This redundancy between the central and local file headers was perhaps designed in order to allow PKZip not to have to keep the entire central directory in memory during extraction. Instead, as each file was extracted, the names and other information could be read from the local headers. Additionally, the local headers can be useful for recovering files from a Zip archive where the central directory is missing or corrupted. However, this redundancy is also a major source of ambiguity. For example, what happens when the filenames in the central and local headers mismatch? Such ambiguities often lead to bugs and security problems.
Not everything from the Central File Header is replicated, though. For example, there are no fields for the file's attributes. Also, if the third least significant bit of gp_flags is set, the CRC-32, compressed and uncompressed size fields will be set to zero, and that information will instead be found in a Data Descriptor block after the file's data (not covered here). This allows writing the LFH before knowing how large the member file is or what size it will compress to.
The Local File Header starts with the signature 'P', 'K', 3, 4, and then has the following structure:
/* Local File Header. */
struct lfh {
uint16_t extract_ver;
uint16_t gp_flag;
uint16_t method;
uint16_t mod_time;
uint16_t mod_date;
uint32_t crc32;
uint32_t comp_size;
uint32_t uncomp_size;
uint16_t name_len;
uint16_t extra_len;
const uint8_t *name;
const uint8_t *extra;
};
The functions below read and write LFHs similarly to the other data structures:
/* Size of a Local File Header, not including name and extra. */
#define LFH_BASE_SZ 30
#define LFH_SIGNATURE 0x04034b50 /* "PK\3\4" little-endian. */
static bool read_lfh(struct lfh *lfh, const uint8_t *src, size_t src_len,
size_t offset)
{
const uint8_t *p;
uint32_t signature;
if (offset > src_len || src_len - offset < LFH_BASE_SZ) {
return false;
}
p = &src[offset];
signature = READ32(p);
if (signature != LFH_SIGNATURE) {
return false;
}
lfh->extract_ver = READ16(p);
lfh->gp_flag = READ16(p);
lfh->method = READ16(p);
lfh->mod_time = READ16(p);
lfh->mod_date = READ16(p);
lfh->crc32 = READ32(p);
lfh->comp_size = READ32(p);
lfh->uncomp_size = READ32(p);
lfh->name_len = READ16(p);
lfh->extra_len = READ16(p);
lfh->name = p;
lfh->extra = lfh->name + lfh->name_len;
assert(p == &src[offset + LFH_BASE_SZ] && "All fields read.");
if (src_len - offset - LFH_BASE_SZ < lfh->name_len + lfh->extra_len) {
return false;
}
return true;
}
static size_t write_lfh(uint8_t *dst, const struct lfh *lfh)
{
uint8_t *p = dst;
WRITE32(p, LFH_SIGNATURE);
WRITE16(p, lfh->extract_ver);
WRITE16(p, lfh->gp_flag);
WRITE16(p, lfh->method);
WRITE16(p, lfh->mod_time);
WRITE16(p, lfh->mod_date);
WRITE32(p, lfh->crc32);
WRITE32(p, lfh->comp_size);
WRITE32(p, lfh->uncomp_size);
WRITE16(p, lfh->name_len);
WRITE16(p, lfh->extra_len);
assert(p - dst == LFH_BASE_SZ);
if (lfh->name_len != 0) {
memcpy(p, lfh->name, lfh->name_len);
p += lfh->name_len;
}
if (lfh->extra_len != 0) {
memcpy(p, lfh->extra, lfh->extra_len);
p += lfh->extra_len;
}
return (size_t)(p - dst);
}
Zip Reader Implementation
Using the functions above, we provide a function to read a Zip file in memory and get an iterator for accessing the members:
typedef size_t zipiter_t; /* Zip archive member iterator. */
typedef struct zip_t zip_t;
struct zip_t {
uint16_t num_members; /* Number of members. */
const uint8_t *comment; /* Zip file comment (not terminated). */
uint16_t comment_len; /* Zip file comment length. */
zipiter_t members_begin; /* Iterator to the first member. */
zipiter_t members_end; /* Iterator to the end of members. */
const uint8_t *src;
size_t src_len;
};
/* Initialize zip based on the source data. Returns true on success, or false
if the data could not be parsed as a valid Zip file. */
bool zip_read(zip_t *zip, const uint8_t *src, size_t src_len)
{
struct eocdr eocdr;
struct cfh cfh;
struct lfh lfh;
size_t i, offset;
const uint8_t *comp_data;
zip->src = src;
zip->src_len = src_len;
if (!find_eocdr(&eocdr, src, src_len)) {
return false;
}
if (eocdr.disk_nbr != 0 || eocdr.cd_start_disk != 0 ||
eocdr.disk_cd_entries != eocdr.cd_entries) {
return false; /* Cannot handle multi-volume archives. */
}
zip->num_members = eocdr.cd_entries;
zip->comment = eocdr.comment;
zip->comment_len = eocdr.comment_len;
offset = eocdr.cd_offset;
zip->members_begin = offset;
/* Read the member info and do a few checks. */
for (i = 0; i < eocdr.cd_entries; i++) {
if (!read_cfh(&cfh, src, src_len, offset)) {
return false;
}
if (cfh.gp_flag & 1) {
return false; /* The member is encrypted. */
}
if (cfh.method != ZIP_STORE &&
cfh.method != ZIP_SHRINK &&
cfh.method != ZIP_REDUCE1 &&
cfh.method != ZIP_REDUCE2 &&
cfh.method != ZIP_REDUCE3 &&
cfh.method != ZIP_REDUCE4 &&
cfh.method != ZIP_IMPLODE &&
cfh.method != ZIP_DEFLATE) {
return false; /* Unsupported compression method. */
}
if (cfh.method == ZIP_STORE &&
cfh.uncomp_size != cfh.comp_size) {
return false;
}
if (cfh.disk_nbr_start != 0) {
return false; /* Cannot handle multi-volume archives. */
}
if (memchr(cfh.name, '\0', cfh.name_len) != NULL) {
return false; /* Bad filename. */
}
if (!read_lfh(&lfh, src, src_len, cfh.lfh_offset)) {
return false;
}
comp_data = lfh.extra + lfh.extra_len;
if (cfh.comp_size > src_len - (size_t)(comp_data - src)) {
return false; /* Member data does not fit in src. */
}
offset += CFH_BASE_SZ + cfh.name_len + cfh.extra_len +
cfh.comment_len;
}
zip->members_end = offset;
return true;
}
As hinted at above, member iterators are really just Central File Header offsets, through which the members data can be accessed:
typedef enum {
ZIP_STORE = 0,
ZIP_SHRINK = 1,
ZIP_REDUCE1 = 2,
ZIP_REDUCE2 = 3,
ZIP_REDUCE3 = 4,
ZIP_REDUCE4 = 5,
ZIP_IMPLODE = 6,
ZIP_DEFLATE = 8
} method_t;
typedef struct zipmemb_t zipmemb_t;
struct zipmemb_t {
const uint8_t *name; /* Member name (not null terminated). */
uint16_t name_len; /* Member name length. */
time_t mtime; /* Modification time. */
uint32_t comp_size; /* Compressed size. */
const uint8_t *comp_data; /* Compressed data. */
uint16_t made_by_ver; /* Made-by version, e.g. 20 for PKZip 2.0. */
method_t method; /* Compression method. */
bool imp_large_wnd; /* For implode: compressed with 8K window? */
bool imp_lit_tree; /* For implode: Huffman coded literals? */
uint32_t uncomp_size; /* Uncompressed size. */
uint32_t crc32; /* CRC-32 checksum. */
const uint8_t *comment; /* Comment (not null terminated). */
uint16_t comment_len; /* Comment length. */
bool is_dir; /* Whether this is a directory. */
zipiter_t next; /* Iterator to the next member. */
};
/* Get the Zip archive member through iterator it. */
zipmemb_t zip_member(const zip_t *zip, zipiter_t it)
{
struct cfh cfh;
struct lfh lfh;
bool ok;
zipmemb_t m;
assert(it >= zip->members_begin && it < zip->members_end);
ok = read_cfh(&cfh, zip->src, zip->src_len, it);
assert(ok);
ok = read_lfh(&lfh, zip->src, zip->src_len, cfh.lfh_offset);
assert(ok);
(void)ok;
m.name = cfh.name;
m.name_len = cfh.name_len;
m.mtime = dos2ctime(cfh.mod_date, cfh.mod_time);
m.comp_size = cfh.comp_size;
m.comp_data = lfh.extra + lfh.extra_len;
m.method = cfh.method;
m.made_by_ver = cfh.made_by_ver;
m.imp_large_wnd = (m.method == ZIP_IMPLODE) ? (cfh.gp_flag & 2) : false;
m.imp_lit_tree = (m.method == ZIP_IMPLODE) ? (cfh.gp_flag & 4) : false;
m.uncomp_size = cfh.uncomp_size;
m.crc32 = cfh.crc32;
m.comment = cfh.comment;
m.comment_len = cfh.comment_len;
m.is_dir = (cfh.ext_attrs & EXT_ATTR_DIR) != 0;
m.next = it + CFH_BASE_SZ +
cfh.name_len + cfh.extra_len + cfh.comment_len;
assert(m.next <= zip->members_end);
return m;
}
Zip Writer Implementation
To write a Zip file into a memory buffer, we first need to know how much memory to allocate. Since we do not know how much the data will compress before we try it, we calculate an upper bound by using the uncompressed member sizes:
/* Compute an upper bound on the dst size required by zip_write() for an
* archive with num_memb members with certain filenames, sizes, and archive
* comment. Returns zero on error, e.g. if a filename is longer than 2^16-1, or
* if the total file size is larger than 2^32-1. */
uint32_t zip_max_size(uint16_t num_memb, const char *const *filenames,
const uint32_t *file_sizes, const char *comment)
{
size_t comment_len, name_len;
uint64_t total;
uint16_t i;
comment_len = (comment == NULL ? 0 : strlen(comment));
if (comment_len > UINT16_MAX) {
return 0;
}
total = EOCDR_BASE_SZ + comment_len; /* EOCDR */
for (i = 0; i < num_memb; i++) {
assert(filenames[i] != NULL);
name_len = strlen(filenames[i]);
if (name_len > UINT16_MAX) {
return 0;
}
total += CFH_BASE_SZ + name_len; /* Central File Header */
total += LFH_BASE_SZ + name_len; /* Local File Header */
total += file_sizes[i]; /* Uncompressed data size. */
}
if (total > UINT32_MAX) {
return 0;
}
return (uint32_t)total;
}
The code below writes a Zip file using Deflate compression for each member where that yields a smaller size:
/* Write a Zip file containing num_memb members into dst, which must be large
enough to hold the resulting data. Returns the number of bytes written, which
is guaranteed to be less than or equal to the result of zip_max_size() when
called with the corresponding arguments. The years in mtimes will be clamped
between 1980 and 2107, comment shall be a null-terminated string or null,
callback shall be null or point to a function which will get called
after the compression of each member. */
uint32_t zip_write(uint8_t *dst, uint16_t num_memb,
const char *const *filenames,
const uint8_t *const *file_data,
const uint32_t *file_sizes,
const time_t *mtimes,
const char *comment,
method_t method,
void (*callback)(const char *filename, method_t method,
uint32_t size, uint32_t comp_size))
{
uint16_t i;
uint8_t *p;
struct eocdr eocdr;
struct cfh cfh;
struct lfh lfh;
bool ok;
uint16_t name_len;
uint8_t *data_dst;
size_t data_dst_sz, comp_sz;
uint32_t lfh_offset, cd_offset, eocdr_offset;
p = dst;
/* Write Local File Headers and compressed or stored data. */
for (i = 0; i < num_memb; i++) {
assert(filenames[i] != NULL);
assert(strlen(filenames[i]) <= UINT16_MAX);
name_len = (uint16_t)strlen(filenames[i]);
data_dst = p + LFH_BASE_SZ + name_len;
data_dst_sz = (file_sizes[i] > 0) ? file_sizes[i] - 1 : 0;
if (method == ZIP_SHRINK && file_sizes[i] > 0 &&
hwshrink(file_data[i], file_sizes[i],
data_dst, data_dst_sz, &comp_sz)) {
lfh.method = ZIP_SHRINK;
assert(comp_sz <= UINT32_MAX);
lfh.comp_size = (uint32_t)comp_sz;
lfh.gp_flag = 0;
lfh.extract_ver = (0 << 8) | 10; /* DOS | PKZip 1.0 */
} else if (method >= ZIP_REDUCE1 && method <= ZIP_REDUCE4 &&
hwreduce(file_data[i], file_sizes[i],
(int)(method - ZIP_REDUCE1 + 1),
data_dst, data_dst_sz, &comp_sz)) {
lfh.method = (uint16_t)method;
assert(comp_sz <= UINT32_MAX);
lfh.comp_size = (uint32_t)comp_sz;
lfh.gp_flag = 0;
lfh.extract_ver = (0 << 8) | 10; /* DOS | PKZip 1.0 */
} else if (method == ZIP_IMPLODE &&
hwimplode(file_data[i], file_sizes[i],
/*large_wnd=*/true, /*lit_tree=*/true,
data_dst, data_dst_sz, &comp_sz)) {
lfh.method = ZIP_IMPLODE;
assert(comp_sz <= UINT32_MAX);
lfh.comp_size = (uint32_t)comp_sz;
lfh.gp_flag = (0x1 << 1); /* large_wnd */
lfh.gp_flag |= (0x1 << 2); /* lit_tree */
lfh.extract_ver = (0 << 8) | 10; /* DOS | PKZip 1.0 */
} else if (method == ZIP_DEFLATE &&
hwdeflate(file_data[i], file_sizes[i],
data_dst, data_dst_sz, &comp_sz)) {
lfh.method = ZIP_DEFLATE;
assert(comp_sz <= UINT32_MAX);
lfh.comp_size = (uint32_t)comp_sz;
lfh.gp_flag = (0x1 << 1);
lfh.extract_ver = (0 << 8) | 20; /* DOS | PKZip 2.0 */
} else {
memcpy(data_dst, file_data[i], file_sizes[i]);
lfh.method = ZIP_STORE;
lfh.comp_size = file_sizes[i];
lfh.gp_flag = 0;
lfh.extract_ver = (0 << 8) | 10; /* DOS | PKZip 1.0 */
}
if (callback != NULL) {
callback(filenames[i], lfh.method,
file_sizes[i], lfh.comp_size);
}
ctime2dos(mtimes[i], &lfh.mod_date, &lfh.mod_time);
lfh.crc32 = crc32(file_data[i], file_sizes[i]);
lfh.uncomp_size = file_sizes[i];
lfh.name_len = name_len;
lfh.extra_len = 0;
lfh.name = (const uint8_t*)filenames[i];
p += write_lfh(p, &lfh);
p += lfh.comp_size;
}
assert((size_t)(p - dst) <= UINT32_MAX);
cd_offset = (uint32_t)(p - dst);
/* Write the Central Directory based on the Local File Headers. */
lfh_offset = 0;
for (i = 0; i < num_memb; i++) {
ok = read_lfh(&lfh, dst, SIZE_MAX, lfh_offset);
assert(ok);
(void)ok;
cfh.made_by_ver = lfh.extract_ver;
cfh.extract_ver = lfh.extract_ver;
cfh.gp_flag = lfh.gp_flag;
cfh.method = lfh.method;
cfh.mod_time = lfh.mod_time;
cfh.mod_date = lfh.mod_date;
cfh.crc32 = lfh.crc32;
cfh.comp_size = lfh.comp_size;
cfh.uncomp_size = lfh.uncomp_size;
cfh.name_len = lfh.name_len;
cfh.extra_len = 0;
cfh.comment_len = 0;
cfh.disk_nbr_start = 0;
cfh.int_attrs = 0;
cfh.ext_attrs = EXT_ATTR_ARC;
cfh.lfh_offset = lfh_offset;
cfh.name = lfh.name;
p += write_cfh(p, &cfh);
lfh_offset += LFH_BASE_SZ + lfh.name_len + lfh.comp_size;
}
assert((size_t)(p - dst) <= UINT32_MAX);
eocdr_offset = (uint32_t)(p - dst);
/* Write the End of Central Directory Record. */
eocdr.disk_nbr = 0;
eocdr.cd_start_disk = 0;
eocdr.disk_cd_entries = num_memb;
eocdr.cd_entries = num_memb;
eocdr.cd_size = eocdr_offset - cd_offset;
eocdr.cd_offset = cd_offset;
eocdr.comment_len = (uint16_t)(comment == NULL ? 0 : strlen(comment));
eocdr.comment = (const uint8_t*)comment;
p += write_eocdr(p, &eocdr);
assert((size_t)(p - dst) <= zip_max_size(num_memb, filenames,
file_sizes, comment));
return (uint32_t)(p - dst);
}
HWZip
We now know how to read and write Zip files, and how to compress and decompress the data stored within. Let us write a simple Zip program to put it all together. The code is available in hwzip.c.
We will use a macro for simple error handling, and a few helper functions for checked memory allocation:
#define PERROR_IF(cnd, msg) do { if (cnd) { perror(msg); exit(1); } } while (0)
static void *xmalloc(size_t size)
{
void *ptr = malloc(size);
PERROR_IF(ptr == NULL, "malloc");
return ptr;
}
static void *xrealloc(void *ptr, size_t size)
{
ptr = realloc(ptr, size);
PERROR_IF(ptr == NULL, "realloc");
return ptr;
}
Another two functions are used for reading and writing files:
static uint8_t *read_file(const char *filename, size_t *file_sz)
{
FILE *f;
uint8_t *buf;
size_t buf_cap;
f = fopen(filename, "rb");
PERROR_IF(f == NULL, "fopen");
buf_cap = 4096;
buf = xmalloc(buf_cap);
*file_sz = 0;
while (feof(f) == 0) {
if (buf_cap - *file_sz == 0) {
buf_cap *= 2;
buf = xrealloc(buf, buf_cap);
}
*file_sz += fread(&buf[*file_sz], 1, buf_cap - *file_sz, f);
PERROR_IF(ferror(f), "fread");
}
PERROR_IF(fclose(f) != 0, "fclose");
return buf;
}
static void write_file(const char *filename, const uint8_t *data, size_t n)
{
FILE *f;
f = fopen(filename, "wb");
PERROR_IF(f == NULL, "fopen");
PERROR_IF(fwrite(data, 1, n, f) != n, "fwrite");
PERROR_IF(fclose(f) != 0, "fclose");
}
Our Zip program can be used to perform three functions: to list the contents of, extract, or create a Zip file. Listing is easiest:
static void list_zip(const char *filename)
{
uint8_t *zip_data;
size_t zip_sz;
zip_t z;
zipiter_t it;
zipmemb_t m;
printf("Listing ZIP archive: %s\n\n", filename);
zip_data = read_file(filename, &zip_sz);
if (!zip_read(&z, zip_data, zip_sz)) {
printf("Failed to parse ZIP file!\n");
exit(1);
}
if (z.comment_len != 0) {
printf("%.*s\n\n", (int)z.comment_len, z.comment);
}
for (it = z.members_begin; it != z.members_end; it = m.next) {
m = zip_member(&z, it);
printf("%.*s\n", (int)m.name_len, m.name);
}
printf("\n");
free(zip_data);
}
Extraction is slightly more involved. We will use a helper function in zip.c to decompress a member. Besides Deflate, it also handles the legacy compression methods discussed in the follow-up article.
/* Extract a zip member into dst. Returns true on success. The CRC-32 is not
checked. */
bool zip_extract_member(const zipmemb_t *m, uint8_t *dst)
{
size_t src_used, dst_used;
int comp_factor;
switch (m->method) {
case ZIP_STORE:
assert(m->comp_size == m->uncomp_size);
memcpy(dst, m->comp_data, m->comp_size);
return true;
case ZIP_SHRINK:
if (hwunshrink(m->comp_data, m->comp_size, &src_used,
dst, m->uncomp_size, &dst_used)
!= HWUNSHRINK_OK) {
return false;
}
if (src_used != m->comp_size || dst_used != m->uncomp_size) {
return false;
}
return true;
case ZIP_REDUCE1:
case ZIP_REDUCE2:
case ZIP_REDUCE3:
case ZIP_REDUCE4:
comp_factor = (int)m->method - ZIP_REDUCE1 + 1;
if (hwexpand(m->comp_data, m->comp_size, m->uncomp_size,
comp_factor, &src_used, dst) != HWEXPAND_OK) {
return false;
}
if (src_used != m->comp_size) {
return false;
}
return true;
case ZIP_IMPLODE:
/* If the compressed data assumes an incorrect minimum backref
length because of the PKZip 1.01/1.02 bug, the length of the
decompressed data will likely not match the expectations, in
which case we try pk101_bug_compat mode. */
if (hwexplode(m->comp_data, m->comp_size, m->uncomp_size,
m->imp_large_wnd, m->imp_lit_tree,
/*pk101_bug_compat=*/false,
&src_used, dst) == HWEXPLODE_OK &&
src_used == m->comp_size) {
return true;
}
if (hwexplode(m->comp_data, m->comp_size, m->uncomp_size,
m->imp_large_wnd, m->imp_lit_tree,
/*pk101_bug_compat=*/true,
&src_used, dst) == HWEXPLODE_OK &&
src_used == m->comp_size) {
return true;
}
return false;
case ZIP_DEFLATE:
if (hwinflate(m->comp_data, m->comp_size, &src_used,
dst, m->uncomp_size, &dst_used) != HWINF_OK) {
return false;
}
if (src_used != m->comp_size || dst_used != m->uncomp_size) {
return false;
}
return true;
}
assert(0 && "Invalid method.");
return false;
}
A small helper function is used to null-terminate the filename (so it can be passed to fopen):
static char *terminate_str(const char *str, size_t n)
{
char *p = xmalloc(n + 1);
memcpy(p, str, n);
p[n] = '\0';
return p;
}
Our program will skip any archive member that is in a directory. The reason for this is to avoid so called path traversal attacks, where a malicious archive is used to write a file outside the directory specified by the user. See Info-Zip's FAQ for some discussion. Jean-Marc Lienher has a version with directory support on Github.
static void extract_zip(const char *filename)
{
uint8_t *zip_data;
size_t zip_sz;
zip_t z;
zipiter_t it;
zipmemb_t m;
char *tname;
uint8_t *uncomp_data;
printf("Extracting ZIP archive: %s\n\n", filename);
zip_data = read_file(filename, &zip_sz);
if (!zip_read(&z, zip_data, zip_sz)) {
printf("Failed to read ZIP file!\n");
exit(1);
}
if (z.comment_len != 0) {
printf("%.*s\n\n", (int)z.comment_len, z.comment);
}
for (it = z.members_begin; it != z.members_end; it = m.next) {
m = zip_member(&z, it);
if (m.is_dir) {
printf(" (Skipping dir: %.*s)\n",
(int)m.name_len, m.name);
continue;
}
if (memchr(m.name, '/', m.name_len) != NULL ||
memchr(m.name, '\\', m.name_len) != NULL) {
printf(" (Skipping file in dir: %.*s)\n",
(int)m.name_len, m.name);
continue;
}
switch (m.method) {
case ZIP_STORE: printf(" Extracting: "); break;
case ZIP_SHRINK: printf(" Unshrinking: "); break;
case ZIP_REDUCE1:
case ZIP_REDUCE2:
case ZIP_REDUCE3:
case ZIP_REDUCE4: printf(" Expanding: "); break;
case ZIP_IMPLODE: printf(" Exploding: "); break;
case ZIP_DEFLATE: printf(" Inflating: "); break;
}
printf("%.*s", (int)m.name_len, m.name);
fflush(stdout);
uncomp_data = xmalloc(m.uncomp_size);
if (!zip_extract_member(&m, uncomp_data)) {
printf(" Error: decompression failed!\n");
exit(1);
}
if (crc32(uncomp_data, m.uncomp_size) != m.crc32) {
printf(" Error: CRC-32 mismatch!\n");
exit(1);
}
tname = terminate_str((const char*)m.name, m.name_len);
write_file(tname, uncomp_data, m.uncomp_size);
printf("\n");
free(uncomp_data);
free(tname);
}
printf("\n");
free(zip_data);
}
To create a Zip archive, we read the input files and feed them to zip_write. Since the C standard library does not provide a way to get the modification time of a file, we use the current time instead (fixing this is left as an exercise to the reader).
void zip_callback(const char *filename, method_t method,
uint32_t size, uint32_t comp_size)
{
switch (method) {
case ZIP_STORE:
printf(" Stored: "); break;
case ZIP_SHRINK:
printf(" Shrunk: "); break;
case ZIP_REDUCE1:
case ZIP_REDUCE2:
case ZIP_REDUCE3:
case ZIP_REDUCE4:
printf(" Reduced: "); break;
case ZIP_IMPLODE:
printf(" Imploded: "); break;
case ZIP_DEFLATE:
printf(" Deflated: "); break;
}
printf("%s", filename);
if (method != ZIP_STORE) {
assert(size != 0 && "Empty files should use Store.");
printf(" (%.0f%%)", 100 - 100.0 * comp_size / size);
}
printf("\n");
}
static void create_zip(const char *zip_filename, const char *comment,
method_t method, uint16_t n,
const char *const *filenames)
{
time_t mtime;
time_t *mtimes;
uint8_t **file_data;
uint32_t *file_sizes;
size_t file_size, zip_size;
uint8_t *zip_data;
uint16_t i;
printf("Creating ZIP archive: %s\n\n", zip_filename);
if (comment != NULL) {
printf("%s\n\n", comment);
}
mtime = time(NULL);
file_data = xmalloc(sizeof(file_data[0]) * n);
file_sizes = xmalloc(sizeof(file_sizes[0]) * n);
mtimes = xmalloc(sizeof(mtimes[0]) * n);
for (i = 0; i < n; i++) {
file_data[i] = read_file(filenames[i], &file_size);
if (file_size >= UINT32_MAX) {
printf("%s is too large!\n", filenames[i]);
exit(1);
}
file_sizes[i] = (uint32_t)file_size;
mtimes[i] = mtime;
}
zip_size = zip_max_size(n, filenames, file_sizes, comment);
if (zip_size == 0) {
printf("zip writing not possible");
exit(1);
}
zip_data = xmalloc(zip_size);
zip_size = zip_write(zip_data, n, filenames,
(const uint8_t *const *)file_data,
file_sizes, mtimes, comment, method, zip_callback);
write_file(zip_filename, zip_data, zip_size);
printf("\n");
free(zip_data);
for (i = 0; i < n; i++) {
free(file_data[i]);
}
free(mtimes);
free(file_sizes);
free(file_data);
}
Finally, main inspects the command-line arguments and decides what to do:
static void print_usage(const char *argv0)
{
printf("Usage:\n\n");
printf(" %s list <zipfile>\n", argv0);
printf(" %s extract <zipfile>\n", argv0);
printf(" %s create [-m <method>] [-c <comment>] <zipfile> "
" <files...>\n", argv0);
printf("\n");
printf(" Supported compression methods: \n");
printf(" store, shrink, reduce, implode, deflate (default).\n");
printf("\n");
}
static bool parse_method_flag(int argc, char **argv, int *i, method_t *m)
{
if (*i + 1 >= argc) {
return false;
}
if (strcmp(argv[*i], "-m") != 0) {
return false;
}
if (strcmp(argv[*i + 1], "store") == 0) {
*m = ZIP_STORE;
} else if (strcmp(argv[*i + 1], "shrink") == 0) {
*m = ZIP_SHRINK;
} else if (strcmp(argv[*i + 1], "reduce") == 0) {
*m = ZIP_REDUCE4;
} else if (strcmp(argv[*i + 1], "implode") == 0) {
*m = ZIP_IMPLODE;
} else if (strcmp(argv[*i + 1], "deflate") == 0) {
*m = ZIP_DEFLATE;
} else {
print_usage(argv[0]);
printf("Unknown compression method: '%s'.\n", argv[*i + 1]);
exit(1);
}
*i += 2;
return true;
}
static bool parse_comment_flag(int argc, char **argv, int *i, const char **c)
{
if (*i + 1 >= argc) {
return false;
}
if (strcmp(argv[*i], "-c") != 0) {
return false;
}
*c = argv[*i + 1];
*i += 2;
return true;
}
int main(int argc, char **argv)
{
const char *comment = NULL;
method_t method = ZIP_DEFLATE;
int i;
printf("\n");
printf("HWZIP " VERSION " -- A simple ZIP program ");
printf("from https://www.hanshq.net/zip.html\n");
printf("\n");
if (argc == 3 && strcmp(argv[1], "list") == 0) {
list_zip(argv[2]);
} else if (argc == 3 && strcmp(argv[1], "extract") == 0) {
extract_zip(argv[2]);
} else if (argc >= 3 && strcmp(argv[1], "create") == 0) {
i = 2;
while (parse_method_flag(argc, argv, &i, &method) ||
parse_comment_flag(argc, argv, &i, &comment)) {
}
assert(i < argc);
create_zip(argv[i], comment, method, (uint16_t)(argc - i - 1),
(const char *const *)&argv[i + 1]);
} else {
print_usage(argv[0]);
return 1;
}
return 0;
}
Build Instructions
The full set of source files is available in hwzip-2.4.zip. To compile HWZip on Linux or Mac:
$ clang generate_tables.c && ./a.out > tables.c
$ clang -O3 -DNDEBUG -march=native -o hwzip crc32.c deflate.c huffman.c \
hwzip.c implode.c lz77.c reduce.c shrink.c tables.c zip.c
Or on Windows, in a Visual Studio Developer Command Prompt (if you do not have Visual Studio, download the Build Tools):
cl /TC generate_tables.c && generate_tables > tables.c
cl /O2 /DNDEBUG /MT /Fehwzip.exe /TC crc32.c deflate.c huffman.c hwzip.c
implode.c lz77.c reduce.c shrink.c tables.c zip.c /link setargv.obj
(setargv.obj is for expanding wildcard command-line arguments.)
Conclusion
It is fascinating how the evolution of technology is both fast and slow. The Zip format was created 30 years ago based on technology from the fifties and seventies, and while much has changed since then, Zip files are essentially the same and more prevalent than ever. I think it is useful to have a good understanding of how they work.
Exercises
- Make HWZip write each file's modification time rather than the current time when creating archives. Use stat(2) on Linux or Mac, and GetFileTime on Windows. Alternatively, add a command-line flag that allows the user to specify the modification time for the files.
- Using the deflation and inflation code from this article, write a program to create and extract gzip files. The format is a simple wrapper around Deflate-compressed data (normally just one file). It is described in RFC 1952.
- Add callbacks to report progress from the hwdeflate and hwinflate functions. For example, they could invoke the callback after each completed Deflate block and report the number of bytes processed. Use this to add progress indicators to hwzip.
- The Zip reader and writer implementations are designed to work with memory-mapped files. Change HWZip to not use read_file, but mmap(2) on Linux or Mac, and CreateFileMapping on Windows.
- Change HWZip to support extracting and creating archives using the Zip64 format. See the most recent appnote.txt for details.
Further Reading
- For more information about BBS culture, see Jason Scott's BBS: The Documentary. The videos can be found on YouTube. Part 8: Compression covers the SEA vs. PKWare "Arc Wars". The web site has an archive of related historical material. Phil Katz appeared on an episode of Computer Chronicles.
- David Fifield's A better Zip bomb is a great article explaining how to create a Zip file that "explodes" into a very large amount of data when extracted.
- Russ Cox's Zip Files All The Way Down shows how to create a Zip quine, a Zip file which contains a copy of itself.
- Gábor Molnár's ascii-zip is a program that emits a Deflate stream which is entirely ASCII. It was used in Michele Spagnuolo's Rosetta Flash exploit.
- Gynvael Coldwind's Ten Thousand Security Pitfalls: the Zip File Format is a detailed presentation about the format from a security perspective.
- Fabian Giesen's Reading bits in far too many ways part 1, part 2 and part 3 are a great source of information on implementing bitstreams.
- Colton McAnlis and Aleks Haecky's Understanding Compression gives a broad introduction to the subject of data compression.
- Joy Powers' 12 August 2022 Bubbler Talk episode on Milwaukee's National Public Radio covers the history of Zip files.
Linked Files
These are the files linked from this article and their SHA-256 hash values.
| hwzip-1.0.zip | 583fd0ca05bf28f6d7991cc1e7c4eb078389e4957878390d660de4a83cc6486d |
| hwzip-1.1.zip | 480893d4f11f196c33f566247fa221335b3916b4cb231ad1259989ef8e188b8f |
| hwzip-1.2.zip | 780d8f5dd2acc52f150cf4e4396c439280014527995d16c09463a6f1ab42ba8b |
| hwzip-1.3.zip | 32d03b3092fef3cafd99fff231e53fd5452a115978af586a2cf700855866bd52 |
| hwzip-1.4.zip | 8b9f955037ac8ade5a98666429012f88a02a27221d0fc746ab1bc80942fbe011 |
| hwzip-2.0.zip | 2136285dd19024fba551307d3cc32a429e2db9e0fb91f0ce6bf11563efe15510 |
| hwzip-2.1.zip | b2a6fef0d1a564d70b2c9f88b569c17d692c6b531aef9f19a8f830324a7c1f01 |
| hwzip-2.2.zip | 1cde0dab82cf5064f2b89aa204e07eaf6cf2d009cfbba89afd1c8725ddd57c21 |
| hwzip-2.3.zip | 07d364a0fae12cf1ee7bbf72ef3a0e7367ed0fba45027d0eab60f73403efd18f |
| hwzip-2.4.zip | 5a3fecfaf362972673d40ca0611622cfa94170c70029fbd8c9aa64a9e7d387ac |
| pkz193a.exe | c4bf9b677b5776f521f181bc7f036ddeb2fb6ea5c781c8e1d246feb2644b4c8b |
| pkz204g.exe | 004b48f1cdfe0f31888d213e94ae3997aa5fc02bed8a2d75addaf34ae02d1024 |
| winzip1.zip | a894387a28b3155c6ec073402a73788204fe8077b90605c7cad30483ec82da84 |
| wz16v_63.exe | a2e3aadf86d6cb91e8c2119172f1e58fc7fc91381156840514dd1f57c59c07ad |
